Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.1 - Ex. 8
A posição de um carro é dada pelos valores mostrados na tabela.
Encontre a velocidade média para o período de tempo começando quando e durando
Use o gráfico de como uma função de para estimar a velocidade instantânea quando .
Passo 1
Oi galera, tudo bem? O problema nos dá uma tabela com diversos instantes de tempo e suas posições correspondentes.
Queremos determinar a velocidade média para o diversos períodos de tempo, então é bom a gente relembrar como calculamos a velocidade média
É simplesmente a razão entre o deslocamento percorrido em um determinado intervalo de tempo dividido pelo intervalo de tempo correspondente.
A velocidade média entre e será dada por
Beleza? Agora é só aplicar nos instantes pedidos!
Mas relaxa, vou fazer contigo!
Passo 2
Para o primeiro intervalo, começando em e finalizamos em , assim a velocidade média fica:
E usando os dados da tabela:
Tranquilo? Agora vamos repetir esse processo para os outros intervalos! Para e :
E por fim para e :
Percebemos que a velocidade média muda! Sim, vai se aproximando da velocidade instantânea!
Passo 3
Podemos aproximar a velocidade instantânea em a partir da reta tangente ao gráfico nesse ponto. A ideia é plotar os pontos de posição e tempo e traçar uma curva suave entre os pontos. Aí a partir disso, em traçamos uma reta tangente ao gráfico e vemos onde ele passa! Pegando dois pontos, podemos determinar a inclinação!
E sabemos que a inclinação da reta tangente de um gráfico de distância por tempo é a velocidade instantânea!
Bora lá?
A linha pontilhada em azul é a curva suave entre os pontos e a reta pontilhada é a reta tangente.
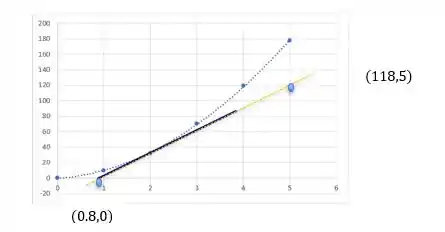
utilizando os pontos que pertencem à reta temos a velocidade instantânea
É isso! Espero ter ajudado!
Resposta