Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.3 - Ex. 5
1-6. Uma partícula move-se segundo a lei do movimento , , onde é medido em segundos e em pés.
- Encontre a velocidade no instante .
- Qual a velocidade depois de s?
- Quando a partícula está em repouso?
- Quando a partícula está se movendo no sentido positivo?
- Encontre a distância total percorrida durante os primeiros segundos.
- Desenhe um diagrama como na figura para ilustrar o movimento da partícula.
5.
Passo 1
Faala meus queridos!
Nessa questão, nos é dado a seguinte função posição para uma partícula:
E a partir dela temos que encontrar a velocidade e depois aplicar o que encontramos nas letras seguintes.Para isso, basta lembrarmos que a derivada de uma função representa a sua taxa de variação. E quando temos uma função posição, ao derivarmos ela com relação ao tempo, vamos obter a função velocidade. Afinal, a velocidade é a taxa de variação temporal da posição, isso é, como a posição varia com o tempo.
Passo 2
a) Encontre a velocidade no instante .
A derivada da função posição, é a velocidade!
Aqui temos uma regra do quociente, aplicando a regra, teremos:
Prontinho.
b) Qual a velocidade depois de s?
Apenas precisamos substituir .
Passo 3
c) Quando a partícula está em repouso?
A partícula vai estar em repouso quando .
A parte de baixo é sempre maior do que zero, podemos retirá-la nesse cálculo!
não pode ser raiz, pois é menor que zero!
(d) Quando a partícula está se movendo no sentido positivo?
A partícula está se movendo no sentido positivo quando .
A parte de baixo é sempre positiva e nunca nula, podemos desconsiderar no estudo do sinal da expressão:
Se é menor que , então é menor que ou maior que .
Porém o não pode ser negativo, então:
Passo 4
(e) Encontre a distância total percorrida durante os primeiros segundos.
Como há uma inversão de sentido em , para calcularmos a distância percorrida, devemos calcular o módulo do deslocamento de até s e depois somar com o módulo do deslocamento de até .
Isso se dá, pois de até s, o deslocamento é positivo, e de até o deslocamento é negativo, mas para a distância percorrida não importa se a partícula anda para frente ou para trás, mas sim o quanto ela anda.
Vamos fazer de até .
A distância percorrida nesse intervalo será:
Vamos fazer de até .
A distância percorrida nesse intervalo será:
Para sabermos a distância percorrida, precisamos apenas somar essas distâncias.
Distância Percorrida é
Passo 5
f) Desenhe um diagrama como na figura para ilustrar o movimento da partícula.
Agora faremos o diagrama!
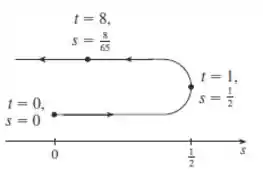
Percebemos que de até , a partícula anda para a frente saindo a posição até .
Depois ela inverte o sentido, andando para trás, e de até sai da posição até .
Resposta
(a)
(b)
(c)
(d)
(e)
Distância Percorrida é
(f)
