Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 72

É possível, às vezes, converter uma integral imprópria em uma integral “própria” com o mesmo valor, através de uma substituição apropriada. Calcule a integral a seguir, fazendo a substituição indicada, e investigue o que acontece se calcularmos a integral diretamente usando um CAS.

∫ 0 1 1 + x 1 - x d x ; u = 1 - x

Passo 1

Vamos reescrever a integral:

∫ 0 1 1 + x 1 - x d x = ∫ 0 1 1 + x 1 - x d x

E usar a substituição do enunciado:

u = 1 - x ∴ u 2 = 1 - x ∴ x = 1 - u 2

d u d x = - 1 2 1 - x ∴ - 2 d u = 1 1 - x d x

u 1 = 1 - 0 = 1 ,   u 2 = 1 - 1 = 0

Substituindo essas coisinhas na integral:

∫ 0 1 1 + x 1 - x d x = - 2 ∫ 1 0 1 + x d u = - 2 ∫ 1 0 2 - u 2 d u = 2 ∫ 0 1 2 - u 2 d u

Passo 2

Agora a gente precisa calcular essa integral. Podemos usar a fórmula 74 da tabela. Fica assim:

2 ∫ 0 1 2 - u 2 d u = 2 u 2 2 - u 2 + 2 2   a r c s e n   u 2   | 1 0 =

= 1 + π 2 = 2 + π 2

Ufa! Belezinha. Chegamos num resultado.

Passo 3

Agora a gente precisa confirmar esse resultado com um CAS. Vamos usar o Wolfram Mathematica para calcular essa integral direto:

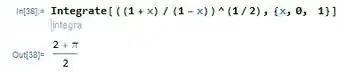
Ih deu igualzinho. Então a gente acertou. Arrasamos!

Resposta

2 + π 2

Mesmo valor nos dois métodos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam α e s , s0 , reais dados. Verifique que ∫ 0 + ∞ e - s ttd t = 1 s 2
Determine m para que ∫ - ∞ + ∞ f xd x = 1 onde f x = m x 2s ex ≤ 1 0s ex1
Sejam α e s , s0 , reais dados. Verifique que ∫ 0 + ∞ e - s te α td t = 1 s - α( sα )
Calcule: ∫ - ∞ + ∞ f ( x )d x Onde f x = 1 1 x 2s ex ≤ 1 s ex1
Utilizando o Exerc. 8, calcule ∫ 0 ∞ e - s tf td t Sendo: f t = sen ⁡ t + 3 cos ⁡ 2 t f t = 3 t + 2 e 3 t + t e t