Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.1 - Ex. 3h

Calcule:

int_(- oo)^(+ oo) f ( x ) d x

Onde

f (x) = {[[1],[(1)/(x^2)]] (s e |x| <= 1)/(s e |x| > 1))

Passo 1

Primeiramente, vamos tentar visualizar essa função no plano, para podermos dividir a integral em algumas integrais.

A função é 1 s e |x| <= 1 , então ela vai ser uma função constante entre - 1 e 1 . Para o restante dos valores a função é 1 // x^2 , vamos esboçar esse gráfico então

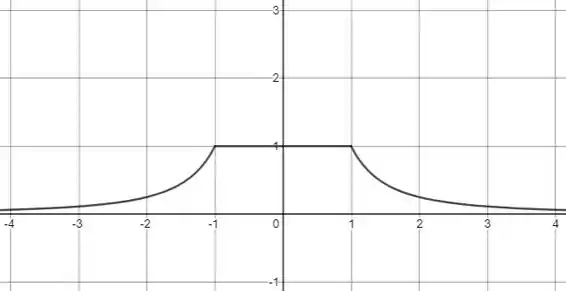
Então podemos dividir nossa integral em três, da seguinte forma

int_(- oo)^(+ oo) f ( x ) d x = int_(- oo)^(- 1) (1)/(x^2) d x + int_(- 1)^1 d x + int_1^(+ oo) (1)/(x^2) d x

Como a função 1 // x^2 é par e simétrica, podemos dizer ainda que

int_(- oo)^(- 1) (1)/(x^2) d x = int_1^(+ oo) (1)/(x^2) d x

Resultando em

int_(- oo)^(+ oo) f ( x ) d x = int_(- 1)^1 d x + 2 int_1^(+ oo) (1)/(x^2) d x

Passo 2

A primeira integral é elementar

int_(- 1)^1 d x = [x]_(- 1)^( 1) = 1 - (- 1) = 2

A segunda integral é uma integral imprópria, então vamos aplicar o limite

int_1^(+ oo) (1)/(x^2) d x = underset(A -> + oo)(lim) int_1^A (1)/(x^2) d x

E agora resolvemos normalmente

underset(A -> + oo)(lim) int_1^A (1)/(x^2) d x = underset(A -> + oo)(lim) int_1^A x^(- 2) d x

underset(A -> + oo)(lim) [(x^(- 1))/(- 1)]_1^A = underset(A -> + oo)(lim) [- (1)/(x)]_1^A

Substituindo os limites de integração

= underset(A -> + oo)(lim) [- (1)/(A) + 1] = 1

Passo 3

Temos então

int_(- oo)^(+ oo) f ( x ) d x = int_(- 1)^1 d x + 2 int_1^(+ oo) (1)/(x^2) d x

int_(- oo)^(+ oo) f ( x ) d x = 2 + 2 * 1

int_(- oo)^(+ oo) f ( x ) d x = 4

Resposta

4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que ∫ 3 ∞e - 3 x d x = 1 3e - 90,000042 e, portanto ∫ 3 ∞e - 3 x d x0,000042 . Explique por que isso significa que podemos substituir o ∫ 0 3 e - x 2 d x por ∫ 0 ∞ e - x 2 d x sem introduzir um
A região do exercício 71 é girada em torno do eixo x e gera um sólido . Determine o Volume do sólido.
A integral S i x = ∫ 0 x s e n t td t é chamada função seno-integral, tem aplicações importantes em óptica.Trace o gráfico do integrando s e n t t para t0 . A função seno-integral é sempre crescente o
A integral S i x = ∫ 0 x s e n t td t é chamada função seno-integral, tem aplicações importantes em óptica.b) Verifique a convergência de ∫ 0 ∞ s e n t td t . Se ela for convergente, qual será seu val
A integral f x = 1 σ 2 πe - 1 2 x - μ σ 2 é chamada função densidade de probabilidade normal, com média μ e desvio padrão σ e tem aplicações importantes em probabilidade e estatística .Calcule ∫ - n n