Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 9
Determine se a curva dada é o gráfico de uma função de . Se for o caso, obtenha o domínio da função e a imagem da função.
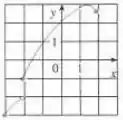
Passo 1
Fala aí! tudo certinho? 😉
Se liga! Como o exercício pede para dizer se o gráfico representa uma função.
Para isso precisamos lembrar que para que tenhamos uma função, cada valor de deve estar associado a um único valor de .
Olhe o gráfico novamente.
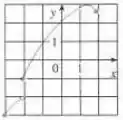
O que você acha? 🤔
Passo 2
Repare que no intervalo todos os elementos de estão associados a um único valor de . Sendo assim, podemos dizer que a figura é sim uma função.
Você pode ficar na dúvida e fazer o seguinte questionamento:
“Quando tem dois valores correspondentes em ().”
Aí vou te perguntar, você reparou que em a bolinha está fechada em e aberta em ?
Sendo assim, podemos dizer que quando , .
Então nada mudou na nossa resposta. O gráfico representa sim uma função.
Tranquilo até aqui? 😎
Passo 3
Já que temos uma função, agora precisamos identificar o domínio e a imagem da função.
Levando em consideração que o domínio são os valores que e ele varia entre e . Podemos escrever o domínio na notação de intervalo como
Concorda? 👀
Passo 4
Já a imagem aqui parece ser mais complicada, mas você vai ver que não é. A imagem pode ser entendida como os valores que assume.
Repare que na figura temos como ponto inicial, da esquerda para a direita, quando , . Depois a linha da função segue até , que é uma bolinha aberta. Este intervalo pode ser escrito como
Para o mesmo que temos uma bolinha aberta em temos uma bolinha fechada em . A partir deste ponto a função continua e atinge seu máximo quando . Podemos escrever este segundo intervalo como
A imagem então será formada pela união entre os dois intervalos que encontramos
E aí! entendeu tudo? Responde Aí! 😉
