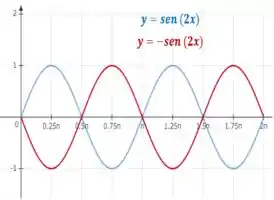
O primeiro gráfico da figura a seguir é aquele que uma calculadora gráfica TI-83 exibe como função . Ele está incorreto e, portanto, para ajudar a explicar sua aparência, redesenhamos a curva em questão no modo pontual da calculadora, obtendo o segundo gráfico.
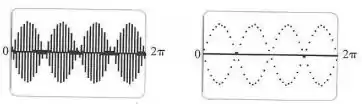
Que duas curvas senoidais a calculadora parece estar desenhando? Mostre que cada ponto do gráfico de que a TI-83 escolhe para desenhar está, de fato, em uma dessas curvas.
Passo 1
Fala aí, pessoal.
Bom, esse problema aqui é mais técnico e envolve o funcionamento de calculadoras gráficas.
Ele mostra dois gráficos pra gente, onde o primeiro é um gráfico na calculadora gráfica TI-83 que exibe como função .

Ele diz que esse gráfico está incorreto e redesenha a curva em questão no modo pontual da calculadora, obtendo o segundo gráfico
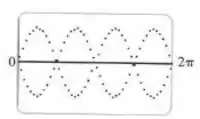
A pergunta é: Que duas curvas senoidais a calculadora parece estar desenhando?
Ou seja, o problema fala de duas curvas combinadas que possuem esse mesmo gráfico.
Ele pede pra gente mostrar que cada ponto do gráfico está, de fato, em uma dessas curvas.
Então teremos que encontrar as combinação de curvas senoidais que possuem esse mesmo comportamento e mostrar que esses pontos também fazem parte dessas curvas.
Show, então bora lá.
Passo 2
No caso, a janela da calculadora TI-83 é de pixels de largura.
Vamos plotar o gráfico no intervalo . Para caber na janela vamos considerar o primento ponto marcado como e o último como , existirão intervalos entre pontos marcados pela calculadora. O tamanho desses intervalos será
Assim, os valores plotados pela calculadora serão nos pontos
Passo 3
Nosso objetivo será encontrar duas funções senos a partir da função que temos.
Quando plotamos , os pontos plotados são:
Mas note que,
E podemos separar o argumento do seno em duas parcelas reescrevendo o como
Assim, o argumento se torna:
E lembrando que
Nossa função se torna:
Logo,
Portanto, os pontos marcados para a curva são os mesmos que os marcados para duas difrentes curvas:
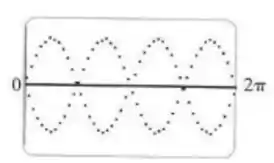
Veja os gráficos:
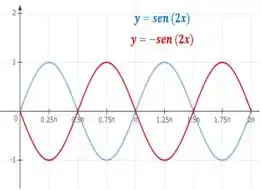
Em comparação com os da calculadora
Resposta