Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 43
Encontre o domínio e esboce o gráfico da função.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente esboce o gráfico e encontre o domínio da seguinte função:
Mas o que é esse domínio??
Bom... Determinar o domínio da função é o mesmo que dizer quais valores de podemos por na função sem que haja nenhum problema. Ou seja, são os valores de para os quais a nossa função está definida.
Só que é mais fácil pensar em quais valores de a função não pode assumir, por isso procuramos sempre por restrições para definir o domínio de uma função. Se ela não tiver nenhuma restrição, seu domínio será todo o conjunto dos números reais.
Dessa forma, vamos sempre analisar se existem valores que deixem um denominador igual a zero ou que façam uma raiz de índice par ter o radicando negativo. Além disso, lembre-se que funções polinomiais, em geral, são definidas para todos os valores de .
Com tudo isso em mente, vamos analisar a nossa função e esboçar seu gráfico no plano cartesiano.
Vamos lá!
Passo 2
Vamos primeiro analisar o domínio, certo?
Observe que temos uma raiz de índice par, que é a raiz quadrada . Pra que essa raiz exista, o valor que tá dentro dela precisa ser sempre positivo, ou seja, precisa ser maior ou igual a zero:
Elevando os dois lados da equação ao quadrado, temos:
E isolando :
Isso significa que a nossa função está definida para todos os valores de maiores ou iguais a . Então, nosso domínio será:
Ou, na notação de intervalo:
Plotando essa curva no plano cartesiano, temos o gráfico:
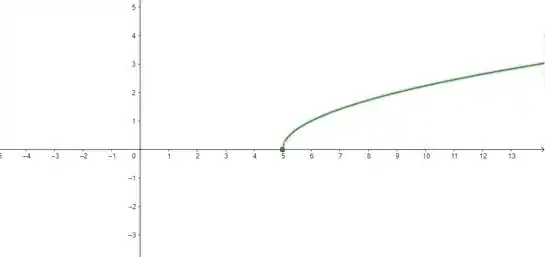
Valeu, galera! Até a próxima! 😉