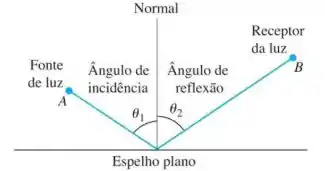
Princípio de Fermat na óptica. A luz de uma fonte é refletida por um espelho plano para um receptor no ponto , como mostra a figura a seguir. Demonstre que para a luz obedecer ao princípio de Fermat o ângulo de incidência deve ser igual ao ângulo de reflexão, medidos a partir da reta normal à superfície refletora do espelho. (Esse resultado pode também ser deduzido sem cálculo. Existe um argumento puramente geométrico, que talvez você prefira.)
Passo 1
Então pessoal, a resposta para essa questão é extremamente intuitiva se pensarmos geometricamente, ok? Desenhando a mesma situação da figura do enunciado, mas com uma situação a mais, que já já será explicada, teremos:
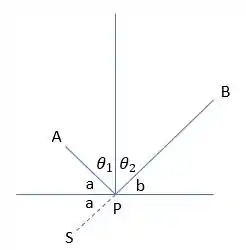
De acordo com a situação mostrada pelo enunciado, o feixe bate em uma superfície refletora no ponto que reflete o mesmo feixe transformando-o em um feixe . Note que as letras mudam só por conta dos sentidos dos feixes, aí fica melhor para analisar o problema.
Passo 2
Agora que construímos a situação, vamos pensar no princípio de Fermat. Esse princípio nos diz que “a trajetória percorrida pela luz ao se propagar de um ponto a outro é tal que o tempo gasto em percorrê-la é um mínimo." Perceba que está falando de mínimo? Para minimizarmos o caminho original do feixe teríamos que pensar no seguinte: a menor distância entre dois pontos é uma reta, certo? Então teria que haver um feixe , que é exatamente o feixe que está pontilhado, que forma uma semireta .
A semireta é igual a uma junção de dois trechos, que é . A consequência disso é que como a semireta é a mesma que a semireta e como os ângulos e são alternos internos, ou seja, são iguais, isso implica que:
E essa é exatamente a relação que estávamos querendo provar!
Resposta
Ei, a resposta está no passo a passo :)