Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.3 - Ex. 22

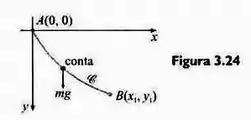
Um problema clássico em cálculo das variações é encontrar a forma de uma curva φ tal que, uma conta, sob a influência da gravidade, escorregue de A 0 ,   0 a B x 1 ,   y 1 em tempo mínimo. Veja a figura 3.24. pode ser mostrado que a equação diferencial para a forma do caminho é y 1 + y ' 2 = k , em que k é uma constante. Primeiro, resolva para d x em termos de y e d y , e então use a substituição y = k . s e n 2 θ para obter a forma paramétrica da solução. A curva φ será uma cicloide.

Passo 1

Então galera, a equação diferencial que nos foi dada é essa aqui:

y 1 + y ' 2 = k

Ou na notação de Leibniz:

y 1 + d y d x 2 = k

Simplificando, teremos:

1 + d y d x 2 = k y

d y d x 2 = k y - 1 = k - y y

d y d x = k - y y

Separando as variáveis:

y k - y d y = d x

Show!

Passo 2

Agora que separamos as variáveis e simplificamos o máximo possível vamos aplicar a substituição proposta pelo enunciado, que é: y = k . s e n 2 θ . Dessa substituição tiramos que:

d y = 2 k . s e n   θ . cos ⁡ θ d ϵ

d y = k s e n   2 θ d θ

Substituindo, teremos:

k . s e n 2 θ k - k . s e n 2 θ k s e n   2 θ d θ = d x

Simplificando:

s e n 2 θ 1 - s e n 2 θ k s e n   2 θ d θ = d x

k s e n   θ cos ⁡ θ . 2 . s e n   θ . cos ⁡ θ . d θ = d x

2 k s e n 2 θ d θ = d x

Como s e n 2 θ = 1 2 1 - cos ⁡ 2 θ , então teremos:

k 1 - cos ⁡ 2 θ d θ = d x

E agora é só integrar e resolver!

Passo 3

Integrando, teremos:

k ∫ d θ - k ∫ cos ⁡ 2 θ = ∫ d x

Para o lado esquerdo teremos:

k ∫ d θ - k ∫ cos ⁡ 2 θ = k θ - 1 2 s e n   2 θ + c 1

Para o lado direito teremos:

∫ d x = x + c 2

Unindo os resultados, teremos como resposta:

k θ - 1 2 s e n   2 θ = x + c

E está aí nossa resolução! 😉

Resposta

k θ - 1 2 s e n   2 θ = x + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada.1. x e 2 y . d y d x + e 2 y = ln ⁡ x x
Uma equação semelhante a do problema 12 é: x . d 2 y d x 2 = v 1 v 2 1 + d y d x 2 Neste caso, a equação surge no estudo da forma do caminho que um perseguidor, correndo a uma velocidade v 2 , deve pe
Dois compostos químicos A e B são combinados para formar um terceiro composto C . A taxa ou velocidade da reação é proporcional à quantidade instantânea de A e B não convertida em C . Inicialmente, há
23. O problema de valor inicial que descreve o movimento de um pêndulo simples com velocidade inicial e ângulo inicial θ 00 é: d 2 θ d t 2 + g l s e nθ = 0 θ 0 = θ 0 ,d θ d t t = 0 = 0 a) Obtenha a eq