Esse problema ilustra o fato de que o autovalor pode aparecer tanto nas condições de contorno quanto na equação diferencial. Considere as vibrações longitudinais de uma barra elástica reta uniforme, de comprimento . Pode-se mostrar que o deslocamento axial satisfaz a equação diferencial parcial

em que E é o módulo de Young e é a massa por unidade de volume. Se a extremidade em estiver fixa, então a condição de contorno aí será

Suponha que a extremidade em está rigidamente presa a uma massa m, mas não tem outras restrições. Podemos obter a condição de contorno aí escrevendo a lei de Newton para a massa. Da teoria de elasticidade, pode-se mostrar que a força exercida na barra pela massa é dada por . Logo, a condição de contorno é

Suponha que . Mostre que e satisfazem equações diferenciais

Mostre que as condições de contorno são

em que é um parâmetro adimensional que fornece a razão entre a massa presa e a massa da barra.

Sugestão: Use a equação diferencial para para simplificar a condição de contorno em .

Determine a forma das autofunções e a equação satisfeita pelos autovalores reais das .

Encontre os dois primeiros autovalores e se .

Vamos considerar como condição inicial

Então pela condição de contorno dada inicialmente teremos:

Onde .

E Considerando que , pela condição , teremos:

Em linhas gerais a equação será:

Só que logo:

Como estamos interessados apenas na variação do comprimento então podemos ignorar , e multiplicando em cima e embaixo na parcela de teremos:

Onde é dito que , logo:

Como

Então a solução para autovalores reais será:

Aplicando a condição , nós teremos que , nos dando uma autofunção igual a:

Agora para

Temos:

Em :

Dividimos tudo por também.

Isolando teremos:

Fazendo teremos:

Como , então:

Então a equação de contorno:

Nos deixando com uma relação para igual a:

Plotando os gráficos de e , nós chegamos

Para teremos o seguinte gráfico:

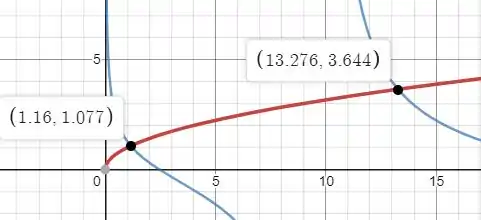
E para

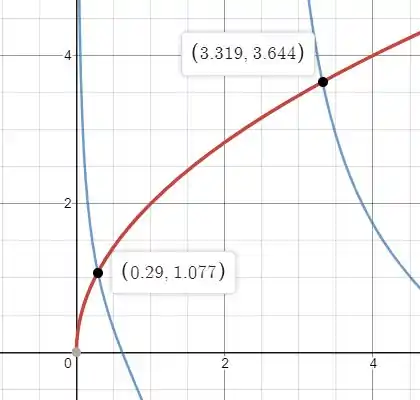
Para

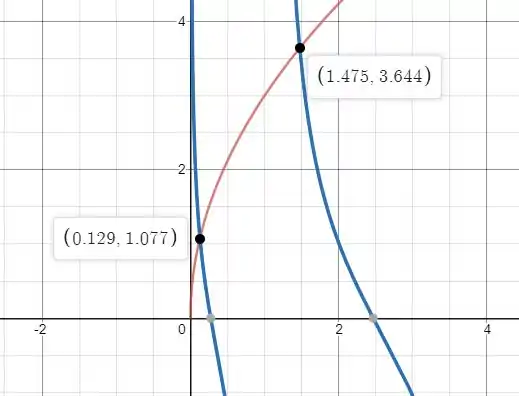
Os valores de na horizontal estarão seguindo a ordem de:

Provar isso analiticamente pode ser um tanto complicado.