Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 7.4 - Ex. 31
Nos problemas 31-38, use o teorema 7.10 para encontrar a transformada de Laplace da função periódica dada.
Passo 1
Salveee cara, bora lá!
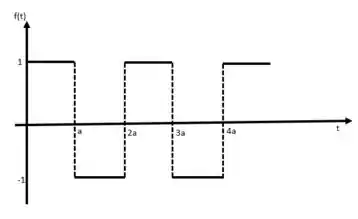
Temos essa função periódica:
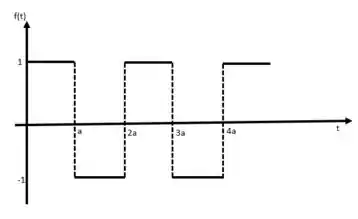
O teorema 7.10 do seu livro fala que quando temos uma função periódica com período , sua transformada vai ser
Então vamos aplicar esse teorema aqui no nosso caso beleza? Afinal, temos uma função periódica com período
Passo 2
Vamos aplicar as informações da nossa função no teorema 7.10:
Resolvendo as integrais:
Arrumando tudo:
Então, temos:
Resposta
Exercícios de Livros Relacionados
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral.13. L t ∫ 0 t s e nτ d τ
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral.15. L 1 * t 3
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral. L { t 2 * t 4 }
Nos problemas 7-20, encontre a transformada de Laplace da função dada sem resolver a integral. L { t 2 * t . e t }
Prove a propriedade comutativa da convolução f * g = g * f