Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 73

Prove analiticamente que se as diagonais de um retângulo forem perpendiculares, então o retângulo será um quadrado.

Passo 1

Queremos provar que se as retas que ligam os vértices opostos de um retângulo (diagonais) forem perpendiculares entre si, ou seja, formarem um ângulo de 90°, então o retângulo possuirá todos os lados iguais (quadrado).

Pare começar, vamos desenhar a situação descrita pelo problema.

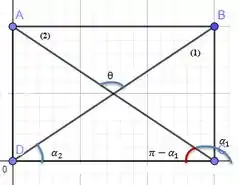
Para resolver o problema precisamos provar que o ângulo entre as diagonais θ é igual a 90°.

Sabendo que:

θ = α 1 - α 2

Precisamos calcular os ângulos α 1 e   α 2 .

Passo 2

Primeiro vamos calcular o ângulo α 1 , por ser um ângulo obtuso:

s e n   α 1 = s e n   π - α 1 = C a t e t o   O p o s t o H i p o t e n u s a

c o s   α 1 = - c o s   π - α 1 = C a t e t o   A d j a c e n t e H i p o t e n u s a

Sendo assim:

t g   α 1 = s e n   α 1 c o s   α 1 = s e n   ( π - α 1 ) - c o s   ( π - α 1 )

Separadamente:

s e n   π - α 1 = A D A C

c o s   π - α 1 = C D A C

Substituindo:

t g   α 1 = A D A C - C D A C = - A D C D

Para o ângulo α 2 :

s e n   α 2 = C a t e t o   O p o s t o H i p o t e n u s a

c o s   α 2 = C a t e t o   A d j a c e n t e H i p o t e n u s a

Sendo assim:

t g   α 2 = s e n   α 2 c o s   α 2

Separadamente:

s e n   α 2 = B C B D

c o s   α 2 = C D B D

Substituindo:

t g   α 1 = B C B D C D B D = B C C D

Com as tangentes podemos calcular o ângulo θ.

Passo 3

Dada a equação para o ângulo:

θ = α 1 - α 2

Podemos aplicar a tangente em ambos os lados:

t g   θ = t g   ( α 1 - α 2 )

A tangente da diferença é dada por:

t g   θ = t g   α 2 - t g   α 1 1 + t g   α 2 . t g   α 1

Como a tangente de 90° não é definida, podemos concluir que:

1 + t g   α 2 . t g   α 1 = 0

t g   α 2 . t g   α 1 = - 1

Substituindo as tangentes:

- A D C D . B C C D = - 1

- A D . B C C D ² = - 1

Sabendo que os lados opostos do retângulo são iguais:

A D = B C

A B = C D

Então:

- A D ² C D ² = - 1

- A D 2 = - C D ²

A D 2 = C D ²

Tirando a raiz em ambos os lados:

A D = C D

Concluindo:

A D = B C = A B = C D

Se todos os lados são iguais temos um quadrado.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O gráfico de y = A s e n ( B x ) tem amplitude _______ e é peródico de período _______.
(a) Encontre uma equação para a família de retas cujos membros têm inclinação m = 3 .(b) Encontre uma equação para o membro da família que passe por ( - 1,3 ) .(c) Esboce os gráficos de alguns membros
Encontre uma equação para a família de retas cujos membros são perpendiculares àqueles do Exercício 1.
(a) Encontre uma equação para a família de retas com corte no eixo y igual a b = 2 .(b) Encontre uma equação para o membro da família cujo ângulo de inclinação é 135 ° .(c) Esboce os gráficos de algun
Encontre uma equação para(a) a família de retas passando pela origem.(b) a família de retas com corte no eixo x igual a a = 1 .(c) a família de retas que passam pelo ponto 1 , - 2 .(d) a família de re