Enunciado

Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 49

Mostre, através das inclinações, que os pontos , , e são vértices de um trapezoide.

Passo 1

Sejam pontos A, B, C e D Inicialmente vamos marcar estes pontos no plano cartesiano e traçar as retas que que contêm os lados do nosso quadrilátero.

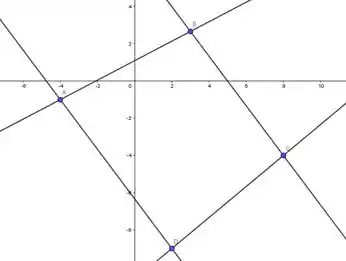
Passo 2

Por definição, trapezoides são quadriláteros que não possuem lados paralelos. Para garantirmos isso, vamos determinar a inclinação das retas que contém cada um dos lados do quadrilátero.

Inclinação da reta que contém os pontos A e B:

Inclinação da reta que contém os pontos B e C:

Inclinação da reta que contém os pontos C e D:

Inclinação da reta que contém os pontos D e A:

Passo 3

Observe que o que garante que os lados não são paralelos. Portanto, o quadrilátero ABCD é um trapezoide, como queríamos mostrar.

Escrever só a resposta aqui quando o problema tiver resposta

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a posição relativa das retas res : r : x , y , z = 1,1 , 1 + λ ( 2,2 , 1 ) s : x , y , z = t ( 1,1 , 0 )

Sejam r 1 : (x, y, z) = (1, 0, 2) + (2t, t, 3t) e r 2 : (x, y, z) = (0, 1, −1) + (t, mt, 2mt) duas retas.(a) Determine m para que as retas sejam coplanares (não sejam reversas). (b) Para o valor de m

(a)Escreva equações da reta paralela à reta x = 2 + λ y = - 1 + 3 λ z = - λ e que corta 0 x no ponto de abscissa 3. (b) Determine a interseção da reta encontrada com o plano z 0 y .

Mostre que, para quaisquer valores de s e t, as retas 2 s + 3 t x + 3 s - 2 t y = 5 s + 4 t passam pelo mesmo ponto. Mostre também que toda reta que passa por esse ponto é representada por uma equação

Determine a e b de modo que as equações x = a t + 1 ,y = b t + 5 sejam uma representação paramétrica da reta y = 2 x + 3 .