Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.5 - Ex. 64
Prove que , mostrando que para todo existe um tal que se então
Passo 1
Pra provar essa afirmação ai galera, vamos primeiro trocar por na expressão da função e definir isso como o valor de N. Logo:
Pra provar que basta substituirmos o valor de escolhido:
E veja só, apareceu! Podemos ainda provar isso numericamente ao escolhermos valores. Seja por exemplo , temos:
Ou seja, qualquer valor de maior que ou menor que que se tome, vai ser maior que . Graficamente:
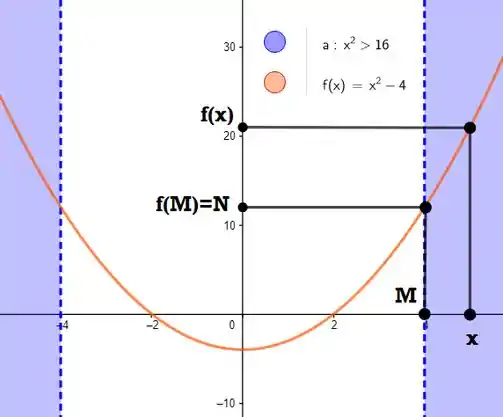
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 5 e 6, explique por que o limite não existe. lim x → 0 x | x |
Determine os limites nos Exercícios 11-22. lim z → 0 2 z - 8 1 3
Determine os limites nos Exercícios 23-42. lim y → 0 5 y 3 + 8 y 2 3 y 4 - 16 y 2
Se f 1 = 5 , lim x → 1 f ( x ) deve existir? Em caso afirmativo, deve ser lim x → 1 f ( x ) = 5 ? Podemos concluir algo sobre lim x → 1 f ( x ) ? Explique.
Determine os limites nos Exercícios 23-42. lim x → 2 x 2 + 12 - 4 x - 2