Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 11
Prove que o triângulo com vértices A(3,-6), B(8,-2) e C(-1,-1) é retângulo. Ache a área do triângulo. (Sugestão: Use o inverso do teorema de Pitágoras)
Passo 1
Fala aii! Pra resolver essa questão, inicialmente vamos marcar os pontos A, B e C no plano cartesiano e fazer o esboço do triângulo.
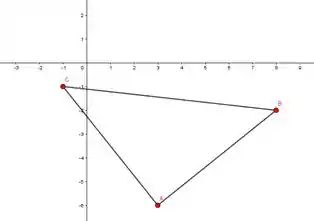
Seja dAB a distância entre os pontos A e B a distâncias entre os pontos A e C e a distância entre os pontos B e C. Para provarmos que o triângulo ABC é retângulo basta mostrarmos que este satisfaz o teorema de Pitágoras, ou seja, que:
Bora começar então!
Passo 2
Vamos determinar cada uma dessas distâncias através da fórmula :
Passo 3
Observe que
Por outro lado
Portanto,
Ou seja, o triângulo ABC é retângulo, como queríamos mostrar.
Passo 4
Agora pra calcular a área vamos usar a clássica:
Resposta
O triângulo ABC é retângulo.