Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 32
Quão rápido estará o ângulo entre o chão e a escada variando no Exemplo quando a parte de baixo da escada estiver a da parede?
Passo 1
Opa, bora resolver esse problema! Queremos saber a que velocidade esta variando o ângulo entre o chão e a escada no exemplo , quando a parte de baixo da escada estiver a da parede. Mas bora resfrescar a memória primeiro!
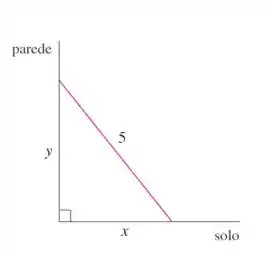
No Exemplo , temos uma escada de metros cuja base desliza afastando-se da parede à taxa de m/s. Seja a altura do topo da escada e a distância da base da escada à parede, temos a seguinte situação:
Passo 2
Assim, temos a relação:
e
Derivando-a em função do tempo:
Passo 3
Quando a parte de baixo da escada estiver a da parede, :
E como m/s então, sua derivada:
Logo, o ângulo decresce (por conta do sinal negativo) a uma taxa de rad/s.
Resposta
O ângulo decresce a uma taxa de rad/s.