Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 83

O movimento de uma mola sujeita a uma força de atrito ou a uma força de amortecimento (tal como um amortecedor em um carro) é frequentemente modelado pelo produto de uma função exponencial e uma função seno ou cosseno. Suponha que a equação de movimento de um ponto dessa mola seja

s t = 2 e - 1,5 t   s e n   2 π t

onde s é medido em centímetros e t , em segundos. Encontre a velocidade após t segundos e faça o gráfico das funções posi��ão e velocidade para 0 ≤ t ≤ 2 .

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente encontrar a velocidade v após t segundos, sabendo que a função posição é dada por:

s t = 2 e - 1,5 t   s e n   2 π t

Além disso, ele pede pra gente esboçar o gráficoda função posição e da velocidade, no intervalo 0 ≤ t ≤ 2 .

Pra isso, a gente precisa lembrar que a velocidade é a derivada da função posição.

Então, o que nós vamos fazer é derivar a função s t = 2 e - 1,5 t   s e n   2 π t e depois esboçar o gráfico de s ( t ) e de v ( t ) , para t ∈ [ 0 ,   2 ] .

Vamos lá!

Passo 2

Vamos começar aplicando a derivada na função posição:

v = d s d t

v = d d t 2 e - 1,5 t   s e n   2 π t

Então, derivando usando a regra do produto e a regra da cadeia, temos:

v = 2 e - 1,5 t ' ∙ sin ⁡ ( 2 π t ) + 2 e - 1,5 t ∙ [ sin ⁡ ( 2 π t ) ] '  

v = - 1,5 ⋅ 2 e - 1,5 t ⋅ sin ⁡ ( 2 π t ) + 2 e - 1,5 t ⋅ cos ⁡ ( 2 π t ) ⋅ 2 π

Assim, calculando os produtos, obtemos nossa velocidade:

v t = 4 π cos ⁡ ( 2 π t ) - 3   sin ⁡ ( 2 π t )   e - 1,5 t

Passo 3

Agora esboçando a função posição, s t = 2 e - 1,5 t sin ⁡ ( 2 π t ) , vamos ter:

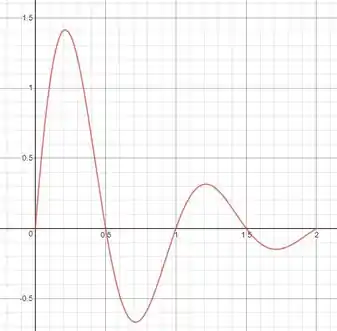
Note que a exponencial modula a amplitude e a função trigonométrica cuida da oscilação.

Passo 4

E esboçando a função velocidade, v t = 4 π cos ⁡ ( 2 π t ) - 3   sin ⁡ ( 2 π t )   e - 1,5 t , temos:

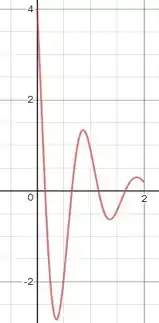
Valeu, galera! Até a próxima! 😉

Resposta

v t = 4 cos ⁡ 2 π t - 3   s e n   2 π t   e - 1,5 t

G r á f i c o s   n o s   p a s s o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

17- Considere as funções dadas por y = a x 2 e y = - x 2 + 1 . Determine a para que os gráficos se interceptem ortogonalmente. (Os gráficos interceptam ortogonalmente em ( x 0 , y 0 ) se as retas tang
18 -Determine a para que as circunferências y 2 + x 2 = 1 e x - a 2 + y 2 = 1 se interceptem ortogonalmente.
16- Com relação ao exercício anterior, supondo π 2απ , expresse d α d t em termos de θe d θ d t .
19 - Mostre que, para todo a , as curvas y = a x 2 e x 2 + 2 y 2 = 1 se interceptam ortogonalmente.
28- Suponha que y = y(t) seja uma função derivável tal que para todo t no seu domínio d y d t = t y 2 .a) Expresse d 2 y d t 2 em termos de t e de y.b) Calcule d 2 y d t 2 | t=1 supondo que y 1 = 1 .