Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 14

14. Fórmula de Galileu para queda livre Galileu desenvolveu uma fórmula para calcular a velocidade de um corpo em queda livre ao rolar bolas a partir do repouso sobre pranchas inclinadas e procurar por uma fórmula limite para prever o comportamento da bola quando a prancha estivesse na vertical e a bola estivesse caindo livremente; veja o item (a) da figura a seguir. Ele descobriu que, para qualquer ângulo da prancha, a velocidade da bola em queda durante t segundos era um múltiplo constante de t. Ou seja, a velocidade era dada por uma fórmula da forma v = kt. O valor da constante k dependia da inclinação da prancha. Em notação moderna - a parte (b) da figura - o que os experimentos de Galileu determinaram foi que a velocidade da bola, com distância em metros e tempo em segundos, para qualquer ângulo θ e com t segundos de rolagem, era

v = 9,8 sen ⁡ θ t   m / s .

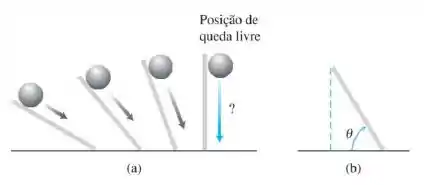
  1. Qual é a equação para a velocidade da bola durante a queda livre?
  2. Usando os dados do item (a), qual é a aceleração constante que um corpo em queda livre experimenta quando está próximo da superfície da Terra?

Passo 1

  1. Para achar a equação da velocidade nesse caso, apenas precisamos substituir os dados na formula:

    O θ , nesse caso, vale 90 ° , pois a prancha esta na posição vertical. Então:

    v = 9,8 sen ⁡ 90 ° t   m / s

    v = 9,8 t   m / s

    Passo 2

Nós sabemos que a aceleração é dada por:

a = d v d t

Então só precisamos derivar a equação da velocidade encontrada no item a

a = 9,8     m / s 2

Passo 2

  1. v = 9,8 t   m / s
  2. a = 9,8     m / s 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma fazenda de piscicultura, uma população de peixes é colocada dentro de um pequeno lago e removida regularmente. Um modelo para a taxa de variação da população é dado pela equação d P d t = r 0 1
No estudo de ecossistemas, o modelo predador-presa é muitas vezes usado para estudar a interação entre as espécies. Considere uma população de lobos da tundra, dada por W ( t ) , e caribus, dada por C
Pesquisadores mediram a concentração média de álcool no sangue C t de oito homens começando uma hora após o consumo de 30m L de etanol (correspondendo a duas bebidas alcoólicas). Faça uma estimativa d
Pesquisadores mediram a concentração média de álcool no sangue C t de oito homens começando uma hora após o consumo de 30m L de etanol (correspondendo a duas bebidas alcoólicas). Encontre a taxa média
A tabela mostra o número de passageiros P que chegaram à Irlanda por avião, em milhões.Determine a taxa média de crescimento de P (i) de 2001 a 2005 (ii) de 2003 a 2005 (iii) de 2005 a 2007 Em cada ca