Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 43

A região delimitada pelas curas dadas é girada em torno do eixo especificado. Ache o volume do solido resultante por qualquer método.

x = y - 1 2 ,   x - y = 1 , em torno de x = - 1

Passo 1

Vamos desenhar as curvas para nos dá uma ideia do que vamos rotacionar, bleza?

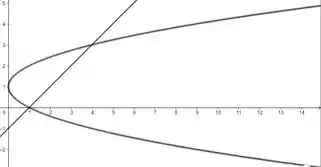
Encontrando as interseções entre as curvas, temos

y + 1 = y - 1 2 ⇒ y + 1 = y 2 - 2 y + 1 ⇒ y = 0   o u   y = 3  

Temos então nossos limites de integração.

Vamos usar discos, ok ?

Passo 2

Temos que

V = π ∫ 0 3 y + 1 - - 1 2 - y - 1 2 - - 1 2 d y  

Ou seja,

V = π ∫ 0 3 y + 2 2 - y 2 - 2 y + 2 2 d y   = π ∫ 0 3 - y 4 + 4 y - 7 y 2 + 12 y d y

Resolvendo a integral,

V = π   - 1 5 y 5 + y 4 - 7 3 y 3 + 6 y 2 0 3 = π - 243 5 + 81 - 63 + 54 = 117 π 5

Resposta

V =   117 π 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Chegamos à Fórmula 6.3.2, V = ∫ a b 2 π x f x d x , utilizando cascas cilíndricas, mas agora podemos usar integração por partes para demonstrá-la usando o método das fatias da Seção 6.2, ao menos para
Use o Teorema de Pappus para encontrar o volume do sólido dado.Uma esfera de raio r (use o Exemplo 4 )
Use o Teorema de Pappus para encontrar o volume do sólido dado.O sólido obtido pela rotação do triângulo com vértices 2 ,3 , 2 ,5 e 5 ,4 ao redor do eixo x .
Use o Teorema de Pappus para encontrar o volume do sólido dado.Um cone com altura h e raio da base r .
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. y = x 3 ,y = 8