Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.1 - Ex. 73

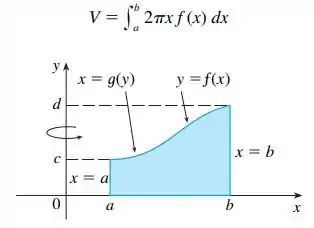
Chegamos à Fórmula 6.3.2, V = ∫ a b 2 π x f x d x , utilizando cascas cilíndricas, mas agora podemos usar integração por partes para demonstrá-la usando o método das fatias da Seção 6.2, ao menos para o caso em que f for injetora e, portanto, tiver uma função inversa g . Use a figura para mostrar que

V = π b 2 d - π a 2 c - ∫ c d π g y 2 d y

Faça a substituição y = f ( x ) e então use integração por partes na integral resultante para demonstrar

Passo 1

Usando a fórmula para volumes de rotação e a figura, nós vemos que

V o l u m e = ∫ 0 d π b 2 d y - ∫ 0 c π a 2 d y - ∫ c d π g y 2 d y = π b 2 d - π a 2 c - ∫ c d π g y 2 d y

Passo 2

Diremos que y = f ( x ) , o que nos dá d y = f ' x d x e g y = x , assim, temos um volume

V = π b 2 d - π a 2 c - π ∫ a b x 2 f ' ( x ) d x

Passo 3

Agora, integrando por partes com u = x 2 , e d v = f ' x d x → d u = 2 x d x ,   v = f ( x ) , e

∫ a b x 2 f ' x d x = x 2 f x a b - ∫ a b 2 x f x d x = b 2 f b - a 2 f a - ∫ a b 2 x f x d x

mas, f a = c e f b = d → V = π b 2 d - π a 2 c - π b 2 d - a 2 c - ∫ a b 2 x f x d x

= ∫ a b 2 π x f x d x

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o segundo teorema de Pappus descrito no exercício 48 para encontrar a área de superfície do toro do exemplo 7.
Prove as fórmulas 9.
Faça com que R seja uma região que fica entre as curvas: y = x m , y = x n , 0 ≤ x ≤ 1 Onde m e n são inteiros com 0 ≤ nm .a) Esboce a região R .b) Encontre as coordenadas do centróide de R .c) Tente
O centróide de uma curva pode ser encontrado por um processo similar ao usado para encontrar o centróide de uma região. Se C é uma curva com comprimento L , então o centróide é ( x - , y - ) onde x -
O segundo teorema de Pappus está na mesma linha do teorema de Pappus da página 565, mas para área de superfície ao invés de volume: Faça com que C seja a curva que fica inteiramente de um lado de uma