Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 39

A região delimitada pelas curvas dadas é girada em torno do eixo especificado . Ache o volume do sólido resultante por qualquer método .

y 2 - x 2 = 1 , y = 2 torno do eixo x .

Passo 1

Opa! Bora calcular o volume de mais um sólido?! O da vez é esse daqui:

y 2 - x 2 = 1 , y = 2 torno do eixo x

Primeiro desenhamos pra ajudar a visualização:

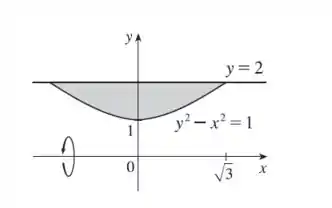
Passo 2

Vamos usar aqui o método das arruelas, portanto o volume do sólido é dado por:

V = π ∫ a b R 2 - r 2   d x

Onde R é a funçãp que limita por cima e r 2 por baixo.

Antes de substituir, isolamos o y na nossa função:

y =   ± x 2 + 1    

Para acharmos nosso limite, precisamos encontrar as intersecções:

2 = x 2 + 1  

4 = x 2 + 1

x = ± 3

Finalmente fazemos:

V = π ∫ - 3 3   2 - 0 2 - x 2 + 1 - 0 2 d x

Reprara que diminuímos zero de cada função, isso porque o nosso eixo de simetria é x = 0 .

V = 2   π   ∫ - 3 3   4 - x 2 + 1 d x  

Por simetria:

V = 2 π ∫ 0 3   ( 3 - x 2 )   d x = 2 π 3 x - 1 3 x 3 0 3

V = 2 π 3 3 - 3  

V = 4   3 π

Resposta

V = 4   3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29–32 Cada integral representa o volume de um sólido. Descreva o sólido.30. 2 π ∫ 0 2 y 1 + y 2 d y
Cada integral representa o volume de um sólido. Descreva o sólido. ∫ 0 1 2 π ( 3 - y ) ( 1 - y 2 ) d y
Cada integral representa o volume de um sólido. Descreva o sólido. ∫ 0 3 2 π x 5 d x