Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.7 - Ex. 72 a

A região do exercício 71 é girada em torno do eixo x e gera um sólido .

  1. Determine o Volume do sólido.

Passo 1

Vamos tentar rotacionar essa curva em relação ao eixo x. Vejamos o gráfico abaixo:

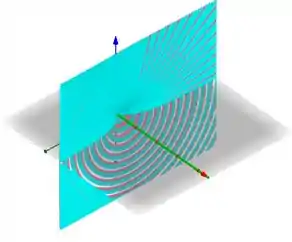
Dá pra notar que ele tem um raio interno e um externo, não é?

Lembre-se que para calcular o volume de um sólido rotacionado em relação ao eixo x , que tem dois raios, usamos a seguinte fórmula,

V = ∫ a b   π ( R x 2 - r x 2 )   d x  

Onde R é o raio externo e r o raio interno da rotação em torno do eixo x .

Passo 2

Vamos tentar encaixar nosso problema à situação acima, beleza?

Dá pra perceber, olhando a figura que nosso R x =     s e c x   e r = t g x  

Agora, vamos definir quem seria nossos limites de integração, beleza?

Como a rotação foi feita com nossa função no intervalo [ 0 , π 2 ] , já temos nossos limites de integração. E nosso volume vai ser dado por:

V =     ∫ 0 π 2     π sec 2 ⁡ x - t g 2 x   d x  

Passo 3

Se olharmos para o gráfico direitinho ou só pensarmos um pouquinho a mais, da pra notar que quando x = π 2 , as funções do integrando não estão bem definidas, então, vamos dá uma mudada na integral. Ou seja,

∫ 0 π 2     s e c x - t g x   d x =   lim b → π 2 ⁡   ∫ 0 b     sec 2 ⁡   x - t g 2 x   d x

Passo 4

Fuçando na memória, temos uma identidade trigonométrica da seguinte forma t g 2 + 1 = sec 2 ⁡ x   . Então, isolando a tangente, nossa integral fica

π ∫ 0 π 2     sec 2 ⁡ x - t g 2 x   d x = π ∫ 0 π 2       sec 2 ⁡ x   - s e x 2 x - 1 d x

Agora ficou fácil, né ? Hhahah

∫ 0 π 2       sec 2 ⁡ x   - s e x 2 x - 1 d x =   ∫ 0 π 2 d x       = π 2 2

Resposta

V = π 2 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 0 ∞ x x 2 + 2 2 d x
Encontre a área sob a curva y = 1 x 3 de x = 1 a x = t e calcule-a para t = 10 , 100 e 1000 . Então, encontre a área total abaixo dessa curva para x ≥ 1 .
Trace as funções f x = 1 x 1,1 e g x = 1 x 0,9 nas janelas retangulares 0,10 por 0,1 e 0,100 por 0,1 .Encontre as áreas sob os gráficos de f e g de x = 1 a x = t e calcule para t = 10 , 100 , 10 4 , 1
Como vimos na seção 3.8, uma substância radioativa decai exponencialmente: a massa no tempo t é m t = m 0e k t , onde m ( 0 ) é a massa inicial e k , uma constante negativa. A vida média M de um átomo
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu