Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 3

Encontre a área sob a curva y = 1 x 3 de x = 1 a x = t e calcule-a para t = 10 , 100 e 1   000 . Então, encontre a área total abaixo dessa curva para x ≥ 1 .

Passo 1

Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Iremos utilizar a integração para calcular a área sob a curva da função dada.

Vamos ter uma visualização de como é a área para t = 10 :

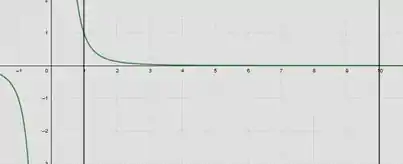
Vemos que a área sob a curva e as retas vai ser dada pela fórmula:

A t = ∫ 1 t x - 3 d x

Passo 2

Essa integral é simples de calcular, vamos calcular a integral indefinida dela, usando uma expressão da Tabela de Integrais Indefinidas:

∫ x n d x = x n + 1 n + 1 + C   n ≠ - 1

Vamos aplicar:

∫ x - 3 d x = x - 3 + 1 - 3 + 1 + C

= x - 2 - 2 + C

= - 1 2 x 2 + C  

Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:

∫ a b f x d x = F b - F a

Vamos lá:

A t = ∫ 1 t x - 3 d x = - 1 2 x 2   1 t

= - 1 2 t 2 - - 1 2 . 1 2

= - 1 2 t 2 + 1 2

Passo 3

Agora é só substituir os valores de t :

A 10 = - 1 2 . 10 2 + 1 2 = 0,495

A 100 = - 1 2 . 100 2 + 1 2 = 0,49995

A 1000 = - 1 2 . 1000 2 + 1 2 = 0,4999995

Passo 4

A área total abaixo da curva x ≥ 1 é:

A t o t a l = ∫ 1 ∞ x - 3 d x =

lim t → ∞ ⁡ - 1 2 t 2 + 1 2 = 1 2

Resposta

A t = - 1 2 t 2 + 1 2

A 10 = 0,495

A 100 = 0,49995

A 1000 = 0,4999995

A t o t a l = 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 25, determine se a integral imprópria é convergente ou divergente. Se for convergente , calcule-a.21. ∫ 1 2 2 d zz l n z 1 5
Nos exercícios de 1 a 25, determine se a integral imprópria é convergente ou divergente. Se for convergente , calcule-a.19. ∫ - 2 2 d x x 3
Nos exercícios de 1 a 25, determine se a integral imprópria é convergente ou divergente. Se for convergente , calcule-a.20. ∫ 0 ∞ e - x d x x
30. Mostre que é possível representar por um número a medida da área da região limitada pela curva cuja equação é y = 1 / x , pela reta x = 1 e pelos eixos x e y ; mas que não é possível representar p
31. Determine se é possível representar por um número a medida do volume do sólido formado pela rotação, em torno do eixo x, da região limitada pela curva cuja equação é y = x - 1 3 , pela reta x = 8