Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 4
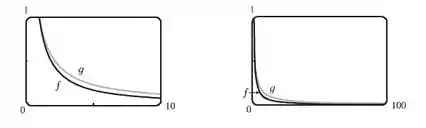
- Trace as funções e nas janelas retangulares por e por .
- Encontre as áreas sob os gráficos de e de a e calcule para , , , , e .
- Calcule a área total sob cada curva para , se ela existir.
Passo 1
- Aqui estão os gráficos das duas funções:
- Vamos calcular área sob o gráfico de de a :
- A área total abaixo da curva de para é:
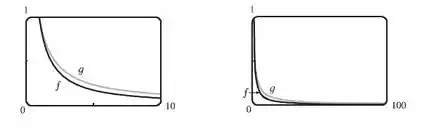
Passo 2
Essa integral é simples de calcular, vamos calcular a integral indefinida dela, usando uma expressão da Tabela de Integrais Indefinidas:
Vamos aplicar:
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá:
Passo 3
Vamos calcular área sob o gráfico de de a :
Essa integral é simples de calcular, vamos calcular a integral indefinida dela, usando uma expressão da Tabela de Integrais Indefinidas:
Vamos aplicar:
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá:
Passo 4
Agora é só substituir os valores de em :
Agora é só substituir os valores de em :
Passo 5
A área total abaixo da curva de para é:
