Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.2 - Ex. 27
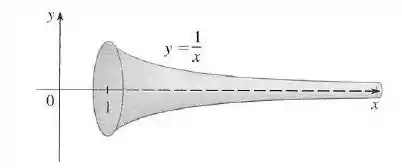
Se a região é girada em torno do eixo , o volume do sólido resultante é finito. Mostre que a área da superfície é infinita.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que a área da superfície é infinita, mesmo o volume desse sólido sendo finito.
Para isso, precisamos lembrar como é a área de uma superfície de revolução, que é da seguinte forma:
Calculando essa integral, vamos analisar o resultado para verificar se a nossa área é de fato infinita.
Vamos lá!
Passo 2
Então, vamos primeiro calcular a derivada :
Agora, vamos inserir esse resultado na raiz do nosso integrando:
Passo 3
Agora, podemos calcular , só substituirmos o que já encontramos no passo anterior:
Antes de calcular esta integral, vamos analisar a raiz no numerador. Observe o seguinte:
Então, temos que :
Simplificando a fração do lado direito da desigualdade:
Mas sabemos que esta integral diverge, portanto, a área de é infinita. Como queríamos demonstrar.
Valeu, galera! Até a próxima! 😉