Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 63
Represente graficamente para . Na mesma tela, esboce o gráfico
Para ; ; ; . Então, em uma nova janela, tente ; e . O que acontece quando ? E quando ? Que fenômeno está sendo ilustrado aqui?
Passo 1
Esta é uma questão que necessita de recursos tecnológicos. Precisamos obter os gráficos de múltiplas funções para entender o que acontece a medida em que diminuímos o valor de . Esta intepretação vai surgir naturalmente a partir do momento em que observarmos as curvas. Entretanto, para poder explicar melhor o fenômeno por trás, vamos relembrar como obtemos a derivada de uma função pela definição. Para isto, calculamos o seguinte limite:
Agora que relembramos este conceito, vamos direto as contas!
Passo 2
O nosso ponto de partida é obter o gráfico das funções e o gráfico da função
Quando ; ; ; . Sendo assim, temos:
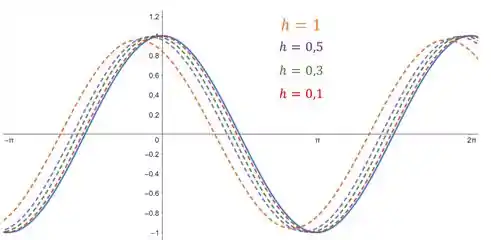
Passo 3
A medida em que diminuímos o valor de , podemos ver que as curvas da função tendem a se sobrepor. Logo, quando
Este resultado era esperado, pois a nossa função nada mais é que a definição de derivada. Portanto, quando , temos a derivada da função , que é a função cosseno.
Passo 4
Vamos agora esboçar os gráficos quando os valores de são negativos. Isto é, ; e . Sendo assim, temos:
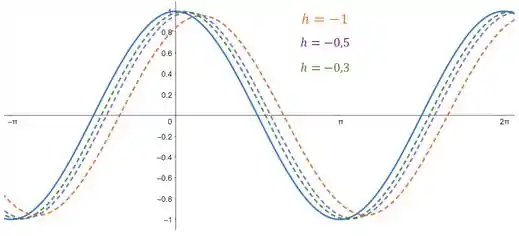
Passo 5
Ao diminuirmos o valor de , fazendo , acontece o mesmo fenômeno que quando . As funções tendem a se sobrepor e no final estamos calculando a derivada da função.
Resposta
Em ambos os casos, a medida em que fazemos , pelo caminho que for, o gráfico da função dada tende a ser o mesmo da função . O fenômeno observado é a derivada da função , o qual é igual a