Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 33
A resistência de uma viga retangular é conjuntamente proporcional à sua largura e ao quadrado de sua profundidade. Ache as dimensões da viga mais resistente que possa ser cortada de uma tora na forma de um cilindro circular reto com cm de raio.
Passo 1
Essas questões têm um jeito bem metódico de resolver, saca só:
- Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil do problema.
- Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
- A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.
Passo 2
Vamos fazer uma coisa de cada vez, primeiro de tudo: dar nome aos bois.
Largura da viga.
Profundidade da viga.
Resistência da viga.
O enunciado diz que a resistência da viga é conjuntamente proporcional à sua largura e ao quadrado de sua profundidade, ou seja:
Perfeito, já temos uma equação para a resistência da viga! Agora precisamos usar algo a mais do enunciado para torar uma função de apenas uma variável.
Passo 3
A questão diz que a viga deve ser cortada de uma tora na forma de cilindro circular reto com 72 cm de raio. Num desenho isso fica:
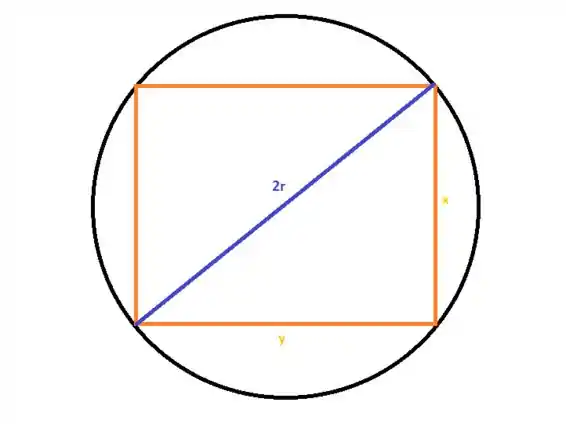
E é o raio da tora em formato de cilindro.
Desse triangulo retângulo que surgiu:
Agora vamos isolar o :
Como :
Agora podemos substituir isso em e ficaremos somente com como variável!
Agora temos a bonitinha com uma variável só! Podemos derivar e encontrar seu ponto de máximo ;)
Passo 4
Derivando :
Agora igualando a e encontrando nosso ponto de máximo:
Como
E GG! Esse é o nosso ponto de máximo. Nesse caso podemos assumir isso pois nessa função o início do intervalo e o final do fechado são zeros. Perceba que e se substituirmos ambos esses valores em ficamos com
Passo 5
Agora precisamos encontrar o valor de , já que a questão pede ambas as dimensões da viga. É só substituir o valor que encontramos de em qualquer uma das funções que tenha essas duas variáveis. Vamos colocar na função que temos de pois o já está isolado e é menos trabalho pra gente hehe.
Prontinho! Já temos ambos os valores de e em função do raio . Agora é só substituir o valor de que a questão nos deu. Fazendo
Resposta
A largura é cm; a espessura é cm.