Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.7 - Ex. 7
Um fazendeiro com 750 pés de cerca quer cercar uma área retangular e então dividi-la em quatro partes com cercas paralelas a um lado do retângulo. Qual é a maior área total possível das quatro partes?
a) Faça vários diagramas ilustrando a situação, alguns com divisões rasas e largas e alguns com divisões profundas e estreitas. Encontre as áreas totais dessas configurações. Parece que existe uma área máxima? Se a resposta for sim, estime-a.
b) Faça um diagrama ilustrando a situação geral. Introduza uma notação e marque no diagrama seus símbolos.
c) Escreva uma expressão para a área total.
d) Use a informação dada para escrever uma equação que relacione as variáveis.
e) Use a parte (d) para escrever a área total como uma função de uma variável.
f) Acabe de resolver o problema e compare sua resposta com sua estimativa na parte (a).
Passo 1
Fala aí, tud belezinha?
Bom, essa questão fala para gente que um fazendeiro com 750 pés de cerca quer cercar uma área retangular e então dividi-la em quatro partes com cercas paralelas a um lado do retângulo.
Teremos que dizer qual é a maior área total possível das quatro partes.
Para isso, o enunciado dá pra gente uma espécie e passos a seguir para encontrar essa resposta. Termos que:
No item a), fazer vários diagramas ilustrando a situação, alguns com divisões rasas e largas e alguns com divisões profundas e estreitas. E encontre as áreas totais dessas configurações.
A ideia aqui é ver se existe uma área máxima, se a resposta for sim, devemos estimá-la.
No item b), vamos fazer um diagrama ilustrando a situação geral. Introduzindo uma notação e marque no diagrama seus símbolos.
No item c) vamos escrever uma expressão para a área total.
O item d) vamos usar a informação dada para escrever uma equação que relacione as variáveis.
No item e) vamos usar a parte (d) para escrever a área total como uma função de uma variável.
E, finalmente no item f), vamos acabar de resolver o problema e comparar nossa resposta com a estimativa do item (a).
Bom, vamos seguir esses passo a passo então.
Vem que te ajudo com isso.
Passo 2
Item a). Vamos escolher algumas formas de fazer o que o fazendeiro quer, mudando os tamanhos das partes da cerca. Queremos fazer um retângulo dividido em 4 como mostra a figura:
Vamos começar com uma largura bem pequena para os retângulos e ir aumentando, pra ver o que acontece com a área. Começaremos com largura 10 e vamos aumentando de 10 em 10. Como temos 8 larguras (4 em cima e 4 em baixo) e 5 alturas, o tamanho da altura será obtido pelo tamanho da largura: . Vamos então fazer os desenhos:
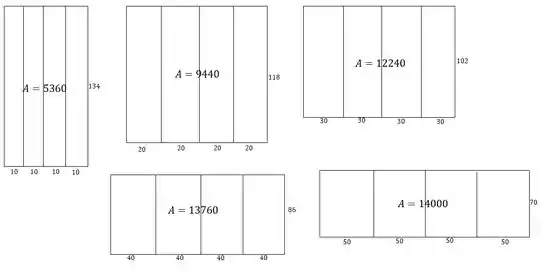
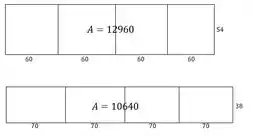
Podemos ver que a área está aumentando e depois começa a diminuir. Parece que existe um valor máximo pra essa área, que ocorre para um valor da largura entre 40 e 60, e que tem valor perto de 14.000 .
Passo 3
Item b). Para o caso geral, como já foi dito no item (a), vamos chamar a espessura dos retângulos de e a altura de . Temos então o diagrama geral:
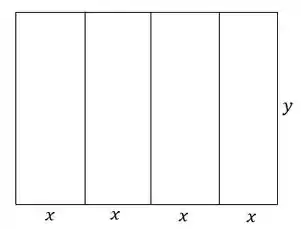
Passo 4
Item c). A área total é a base vezes a altura do retângulo. Temos 4 espessuras na base, então:
Passo 5
Item d). A informação que usamos para relacionar e é o tamanho da cerca, que é 750 pés. Como feito no item (a), temos:
Passo 6
Item e). Calculamos a área total:
Agora usamos a expressão do tamanho da cerca, pra colocar em função de , pra poder substituir na expressão da área:
Substituindo:
Passo 7
Item f). Agora queremos maximizar a função . Pra procurar o valor máximo, devemos achar os pontos críticos da função, que ocorrem quando a derivada é zero ou não existe. Derivando :
Essa derivada sempre existe, então devemos ter pra ter um ponto crítico:
Podemos ver que o valor de está de fato entre 40 e 60 como estimamos. O valor máximo da área é então:
O valor é próximo de 14000 como estimamos.