Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 30

Se os dois lagos iguais de um triângulo isósceles têm comprimento a, encontre o comprimento do terceiro lado que maximiza a área do triangulo.

Passo 1

Eaee, belezinha?? Bom... a questão nos diz que um triângulo isósceles tem os dois lados iguais de comprimento a .

Queremos encontrar o comprimento do terceiro lado x que maximiza a área do triangulo.

Visualmente, temos:

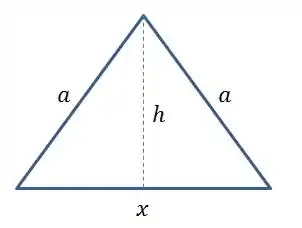
Falou em máximo já sabe né!! Tem derivada igual a zero vindo por aí!!

E aí?? Bora lá?? 😉

Passo 2

Para existir o triângulo, existem algumas condições matemáticas: a soma de dois lados sempre deve ser maior que o terceiro.

a + a > x

a + x > a → e s t e   é   m e i o   o b v i o

A área no triângulo isósceles vai ser dada por:

A = h x 2

Mas por Pitágoras, podemos escrever h como:

h = a 2 - x 2 4

Substituindo na equação da área, temos:

A = x 2 a 2 - x 2 4 ∴

A = 1 2 a 2 x 2 - x 4 4

Passo 3

Derivando a equação de A , temos:

A ' = 1 2 * d d x a 2 x 2 - x 4 4

Aplicando a regra da cadeia, sabemos que:

d y d x = d y d u * d u d x

Fazendo u = a 2 x 2 - x 4 4 , temos:

A ' = 1 2 a 2 x 2 - x 4 4 * d d x a 2 x 2 - x 4 4 ∴

A ' = 1 2 a 2 x 2 - x 4 4 * 2 a 2 x - x 3 ∴

A ' = 2 a 2 - x 2 2 - x 2 + 4 a 2

Passo 4

Igualando a derivada a zero, temos:

A ' = 0 ∴

2 a 2 - x 2 2 - x 2 + 4 a 2 = 0 ∴

2 a 2 - x 2 = 0 ∴

2 a 2 = x 2 ∴

x = ± a 2

Como x não pode ser um valor negativo (comprimento negativo não existe):

x = a 2

Que é o comprimento do terceiro lado que maximiza a área do triângulo!!

Entendeu direitinho?? Responde aee 😉

Resposta

x = a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está para construir uma caixa aberta retangular com base quadrada e um volume de 48p é s ³ é ³. Se o material para o fundo custa $6 / p é s ² é ² e o material para os lados custa $4 / p é s ² é ²
Peste do estanho. Quando o estanho metálico é mantido abaixo de 13,2° C , torna-se lentamente quebradiço e acaba por esfarelar. Se objetos de estanho forem mantidos durante anos a baixas temperaturas,
60. Como tossimos. a. Quando tossimos, a traqueia se contrai e aumenta a velocidade do ar que passa. Isso levanta questões sobre quanto ela deveria se contrair para maximizar a velocidade e se ela rea
50. Trajetória de aterrissagem de um avião. Um avião que voa à altitude H começa a descer rumo à pista de pouso de um aeroporto que está a uma distância terrestre horizontal L do avião, como mostra a
53. Fórmula do tamanho do lote de Wilson. Uma das fórmulas para gerenciamento de almoxarifado diz que o custo médio semanal para você encomendar, pagar e armazenar uma mercadoria é: A q = k m q + c m