Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 39
39. Se lhe for oferecida uma fatia de uma pizza redonda (em outras palavras, um setor de um círculo) e a fatia precisar ter um perímetro de 60 cm, qual diâmetro da pizza vai recompensá-lo com a maior fatia?
Passo 1
Opa, bora pra mais uma questão?! O problema pede pra a gente calcular o diâmetro de uma pizza com fatia de maior área, considerando que o perímetro da fatia é de !
Ficou confuso? O problema só te despertou fome?! Fica tranquilo, vamos esquematizar tudo!
Vamos imaginar essa pizza, e esse tal pedaço aí, ficaria mais ou menos assim:
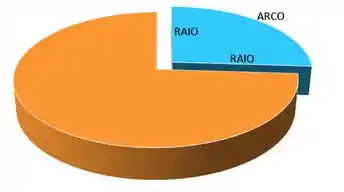
O enunciado disse pra gente que o perímetro dessa fatia vale , esse perímetro é dado por:
Seja o RAIO e o ARCO, temos que:
Podemos relacionar esse arco com o raio, de acordo com o ângulo de abertura. Assim:
Substituindo:
Passo 2
Como queremos a maior fatia de pizza possível, temos que encontrar a maior área possível. A área total da pizza :
E a área da fatia, , será uma sessão dessa área total, que conseguimos relacionar dentro de uma regrinha de 3, tipo assim, a área total é referente ao ângulo de uma volta inteira, , enquanto a área da fatia será referente ao ângulo :
Assim temos:
Substituindo :
Lá em cima vimos que:
Isolando :
Podemos então escrever:
Finalmente chegamos em:
Passo 3
E agora sim, podemos derivar nossa função para encontrar os valores críticos. Bora lá então, derivando temos:
Agora calculamos :
Então quer dizer que o raio da pizza que maximiza o nosso pedaço é dado por , MAAASSSSS ai tem mais uma malandragem, porque queremos o diâmetro e não o raio. Por isso nossa reposta final é
Resposta
O diâmetro é