Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.2 - Ex. 1

Resolva cada um dos problemas de valor inicial a seguir e desenhe os gráficos das soluções para diversos valores de y 0 . Depois descreva, em poucas palavras, as semelhanças e diferenças entre as soluções.

(a) d y d t =   - y + 5   ,       y 0 = y 0

(b) d y d t =   - 2 y + 5   ,       y 0 = y 0

(c) d y d t =   - 2 y + 10   ,       y 0 = y 0

Passo 1

Vamos agora ver como resolvemos edo do seguinte tipo:

d y d t = a y - b

Sabemos que y é função de t, portanto multiplicamos ambos os lados da equação por d t .

d y = a y - b d t ⇒ d y y - b a = a d t   c o m   a ≠ 0

Agora, integramos ambos os lados

∫ d y y - b a = ∫ d t ⇒ ln ⁡ y - b a = a t + C  

⇒ y = c e a t + b a

Repara que para c = 0, temos a solução de equilíbrio.

Caso tenhamos um valor inicial podemos descobrir a constante da solução, por exemplo:

Seja y 0 = y 0

⇒ y 0 = c e a 0 + b a ⇒ c = y 0 - b a

Passo 2

Utilizando do passo 1 para resolver as letras a,b e c, segue que:

(a) d y d t =   - y + 5   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 e - t + 5

(b) d y d t =   - 2 y + 5   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 2 e - 2 t + 5 2

(c) d y d t =   - 2 y + 10   ,       y 0 = y 0

y   = y 0 - b a e a t + b a ⇒   y 0 - 5 e - 2 t + 5

Passo 3

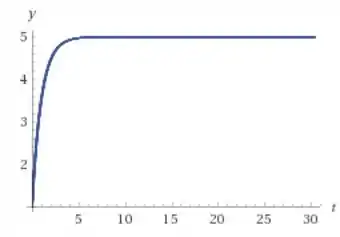
a)

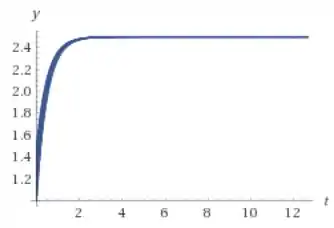
b)

c)

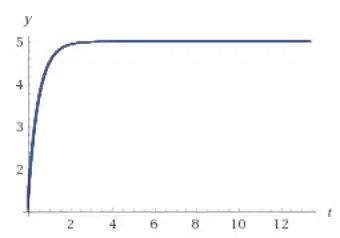
Resposta

A posição de equilíbrio é 5 para as letras (a) e (c) e 5/2 para a letra b, vemos pelos gráfico que a solução tende ao equilíbrio mais rápido em (b) e (c) do que em (a)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha um campo de direção e o adicione aos gráficos das curvas integrais que passam pelos pontos dados. y ' = y 2 ( 0,1 ) ( 0 , 2 ) 0 , - 1 ( 0,0 )
Obtenha um campo de direção e o adicione aos gráficos das curvas integrais que passam pelos pontos dados. y ' = 2 y - 4 ( 0,1 ) ( 0,4 ) 0,5
O exercício não tem solução explícita em termos de funções elementares. Use um SAC para explorar graficamente cada equação diferencial y ' = cos ⁡ ( 2 x - y ) , y 0 = 2 0 ≤ x ≤ 5,0 ≤ y ≤ 5
Obtenha um campo de direção e o adicione ao gráfico da curva integral que passa pelos pontos dados y ' = x y x 2 + 4c o m ( 0 , 2 ) ( 0 , - 6 ) ( - 2 3 , - 4 )
obtenha um campo de direção e trace o gráfico da solução particular ao longo do intervalo especificado. Use seu solucionador SAC para equações diferenciais para encontrar a solução geral da equação di