Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.2 - Ex. 3
Considere a equação diferencial
Em que a e b são números positivos
(a) Encontre a solução geral da equação diferencial
(b) Esboce a solução para diversas condições iniciais
(c) Descreva como a solução muda sob cada uma das seguintes condições
i. a aumenta;
ii. b aumenta;
iii. ambos a e b aumentam mas a razão b/a permanece constante
Passo 1
SALUT, meus jovens gafanhotos! Estamos prestes a ver agora como resolvemos edo do seguinte tipo:
Sabemos que é função de , portanto multiplicamos ambos os lados da equação por
Colocando em “evidência”...
ARRRA! Uma EDO de variáveis separáveis! Integraremos os dois lados para obter então a solução, veja!
Que solução feia! Dentro de logaritmo. Que tal simplificarmos um poquinho aplicando exponencial dos dois lados?
Como é uma constante desconhecida então também será! Podemos então simplesmente trocar por (trocando o desconhecido feio por um desconhecido elegante) rsrs
Repara que para , temos a solução de equilíbrio:
E como e são valores positivos, inevitavelmente, para muito grande (no infinito) teremos a solução de equilíbrio já que vai a .
Mas chega de tagarelar e vamos para o que interessa: o que encontramos aqui foi a solução geral:
Passo 2
Caso tenhamos um valor inicial podemos descobrir a constante da solução dessa EDO, por exemplo:
Seja
Portanto, a condição inicial vai interferir no termo que multiplica o número de neper, de modo que
Para esboçar a solução várias condições iniciais, primeiro vamos dar valores para e de modo que eles sejam positivos (como o problema não nos deu nenhuma condição sobre eles, podemos escolher quais quer valores):
De modo que...
A solução então para o valor inicial é...
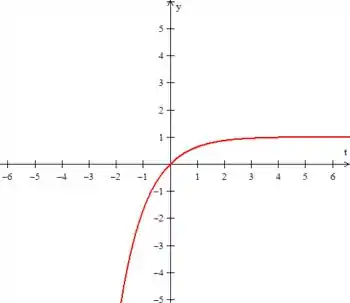
Para ...
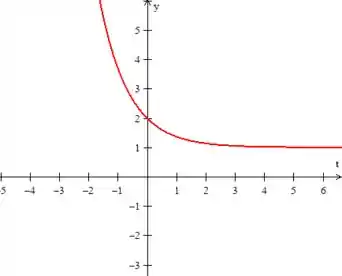
Para ...
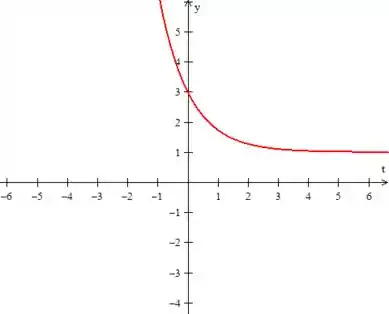
Passo 3
Para esse problema aqui, observe que...
i – aumentando diminuímos a posição de equilíbrio, já que começa a decrescer. Além disso, é aproximado mais rapidamente já que também altera .
ii – aumentando aumentamos a posição de equilíbrio.
iii – o equilíbrio permanece o mesmo, já que é o mesmo, mas como aumenta, podemos falar que a solução é aproximado mais rápido, pelo mesmo motivo em , .
Resposta
a)
b) Para diversos valores de (valor inicial) tem-se uma nova solução:
c)
i – aumentando a diminuímos a posição de equilíbrio e é aproximado mais rapidamente
ii – aumentando b aumentamos a posição de equilíbrio
iii – o equilíbrio permanece o mesmo e é aproximado mais rápido