Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 28
Obtenha um campo de direção e o adicione ao gráfico da curva integral que passa pelos pontos dados
Passo 1
Com o auxílio de um software ou de algum aplicativo que plote campo de direções juntamente com as curvas integrais e, assim, marcaremos os pontos informados nas alternativas. Assim,
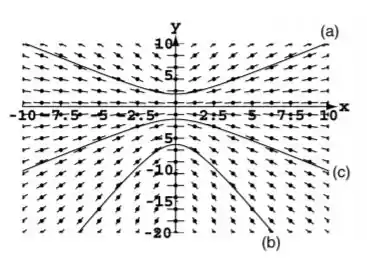
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma equação integral é uma equação que contém uma função desconhecida y(x) e uma integral que envolve y(x). Resolva a determinada equação integral. [Dica: Use uma condição inicial obtida da equação in
(a) Use um sistema de computação algébrica para desenhar um campo de direção para a equação diferencial. Imprima e use-o para esboçar algumas curvas de solução sem resolver aequação diferencial.(b) Re
Uma equação integral é uma equação que contém uma função desconhecida y(x) e uma integral que envolve y(x). Resolva a determinada equação integral. [Dica: Use uma condição inicial obtida da equação in
Encontre a função f tal que f 3 = 2 e t 2 + 1 f ' t + f t 2 + 1 = 0t ≠ 1 [Dica: Use a fórmula de adição para t g( x + y ) na Página de Referência 2.]
Encontre a solução da equação diferencial que satisfaça a condição inicial dada. x ln x = y ( 1 + 3 + y 2 ) y 'y 1 = 1