Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 6
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.
Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada. Uma equação da curva na figura é
6. OBC em torno da reta BC.
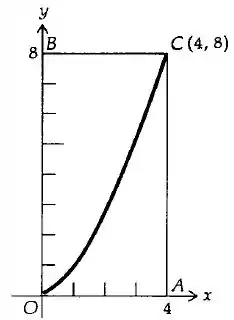
Passo 1
Como essa figura está girando em torno da reta BC, nossa casca cilíndrica imaginária estaria na horizontal e a espessura da casca cilíndrica é dy, então temos que:
Então como o depende de precisamos achar r e h em termos de y.
Assim:
Logo:
Os limites de integração são esses já que y varia de 0 a 8 na região limitada.
Passo 2
Agora basta resolver a integral.
Resposta
Exercícios de Livros Relacionados
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução gerado pela rotação, em torno da reta indicada, da região
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em
1 – 12. Resolva os Exercícios de 5 a 16 da seção 6.1 pelo método do invólucro cilíndrico.Nos Exercícios, ache o volume do sólido de revolução descrito quando a região dada da figura for rotacionada em