Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 21

Nos Exercícios de 21 a 24, a região é limitada pelas curvas e gira em torno do eixo indicado. Ache o volume do sólido gerado.

21. o eixo x

Passo 1

Primeiro vamos ver como fica a região.

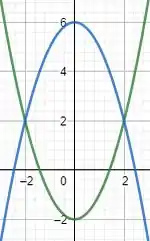
Como essa região está girando em torno do eixo , nossa casca cilíndrica imaginária estaria na horizontal e a espessura da casca cilíndrica é dy, então temos que:

Então como o depende de precisamos achar r e h em termos de y.

Assim:

Mas antes de vermos como a integral para calcular o volume fica, podemos perceber que essa figura é simétrica em relação ao eixo de rotação (x no caso), assim basta avaliar somente a parte superior em rotação, que teremos o mesmo resultado.

Logo:

Os limites de integração são esses já que y na parte superior varia de 0 a 2 na região limitada.

Passo 2

Agora vamos resolver a integral.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o volume do sólido gerado pela rotação em torno do eixo y, da região limitada pelo gráfico de y = x - 3 e pelas retas x = 1 , x = 5 , e y = 0 . Tome os elementos de área retangulares paralelos ao

Ache o volume do sólido de revolução descrito pelo método do invólucro cilíndrico quando a região dada da figura for rotacionada em torno da reta indicada. Uma equação da curva na figura é y 2 = x 3 .

Resolva o Exercício 5 da seção6.1 pelo método do invólucro cilíndrico.

Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = 2 x - 1 ,y = x ,x = 0

Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = 2 - x 2 ,y = x 2 ,x = 0