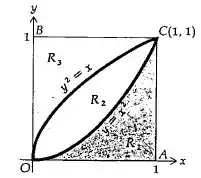
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo y, pela reta y = 1 e pela curva y 2 = x é denotada por R3. Nos Exercícios de 13 a 20, ache o volume do sólido gerado pela rotação da região indicada em torno da reta dada.15. R2 gira em torno do eixo x; os elementos retangulares são paralelos ao eixo de revolução.

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 15

Na Figura abaixo, a região limitada pelo eixo x, pela reta e pela curva é denotada por R1; a região limitada pelas curvas e é denotada por R2; a região limitada pelo eixo y, pela reta e pela curva é denotada por R3. Nos Exercícios de 13 a 20, ache o volume do sólido gerado pela rotação da região indicada em torno da reta dada.

15. R2 gira em torno do eixo x; os elementos retangulares são paralelos ao eixo de revolução.

Passo 1

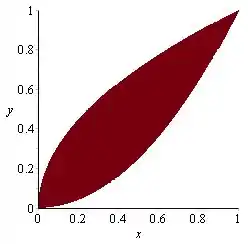
Região R2:

Pode se ter uma ideia do que o enunciado quis dizer com elemento retangular nas figuras 7 e 9 no capítulo 6, seção 2 do livro.

O enunciado pede que os elementos retangulares sejam paralelos ao eixo x de rotação, implica que teremos que usar o método das cascas cilíndricas, então nossa casca cilíndrica estaria na horizontal e a espessura da casca cilíndrica é dy, então temos que:

Então como o depende de precisamos achar r e h em termos de y.

Assim:

Logo:

Os limites de integração são esses já que x varia de 0 a 1 na região R2 limitada.

Passo 2

Agora resolvendo a integral.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um buraco com 2 3 cm de raio é feito através do centro de um sólido esférico com 4 cm de raio. Ache o volume da parte do sólido que foi cortada fora.

Ache o volume do sólido gerado pela rotação da região no primeiro quadrante limitada pela curva y = c o s ( x 2 ) e pelos eixos coordenados em torno do eixo y.

A região no primeiro quadrante, limitada pela curva x = c o s y 2 , pelo eixo y, e pelo eixo x, onde 0 ≤ x ≤ 1 gira em torno do eixo x. Ache o volume do sólido gerado.

Um buraco com 2 cm de raio é feito através de um sólido esférico de 6 cm de raio e o eixo do buraco é um diâmetro da esfera. Ache o volume da parte que sobra da esfera.

Ache o volume do sólido gerado pela rotação da região limitada pela curva x 2 3+y 2 3 = a 2 3 em torno do eixo y.