Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 11c
Resolva a inequação
Passo 1
Para resolver essa inequação, primeiro devemos fazer o estudo do sinal dela. Usando a fórmula para as raízes do exercício . Assim e são:
Como para esse polinômio , e o valor de é:
E usando as fórmulas para as raízes temos:
Então a função troca de sinal nos pontos onde e .
Passo 2
Agora vamos estudar os sinais. O polinômio troca de sinal em e em , então devemos ver os sinais antes e depois desses dois valores.
- Para :
- Para :
Testando para valores menores, por exemplo temos:
Testando para valores maiores, por exemplo temos:
Testando para valores menores, por exemplo , já vimos que a função assume valores negativos
Testando para valores maiores, por exemplo temos:
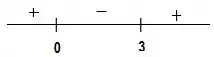
Resumindo temos: antes de positivo, entre e negativo e depois de positivo novamente:
Passo 3
Agora que já temos os sinais, podemos identificar qual é o intervalo de interesse. O problema pede apenas os valores positivos (sem incluir o zero!!) então o intervalo de interesse é antes de e depois de e em ambos lados abertos:
Beleza?