Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 16
16- Seja
a)Esboce o gráfico de .
b) é derivável em Em caso afirmativo, calcule
Passo 1
- Oi, galerinha! Tudo bom? Vamos começar esboçando esse gráfico!
Para , nós temos a equação de uma parábola:
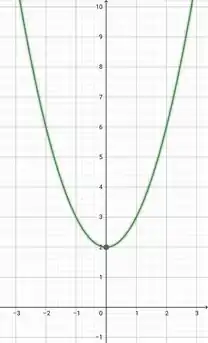
Mas só que para a equação da parábola não serve mais. E o enunciado diz que ela assume um valor constante de . Então, ficamos só com metade da parábola. O resultado é esse gráfico aqui:
Passo 2
b) Gente, para nós sabermos se a nossa função é derivável no ponto , nós temos que usar a definição de derivada:
Lembrem-se que a definição é usada aqui porque a nossa função muda de definição no ponto que nós queremos, sacou ?!
Dessa forma,
Tranquilo, né ?!
Como o limite existe, a função é derivável em , e o valor da derivada é aquele que encontramos para o limite: .
Resposta
a)
b)Sim, a função é derivável em zero. .
Exercícios de Livros Relacionados
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d