Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 7a
Resolva a inequação.
Passo 1
Vamos lá, primeiro vamos tentar manipular um pouco a expressão , vemos que dá pra usar produtos notáveis para destrinchar um pouco, vamo fazer isso então:
Vamos lembrar desse produto notável:
Pronto, se encaixa direitinho na expressão, vamos aplicar então:
Pronto, substituindo temos:
Passo 2
Para estudar o sinal da expressão vamos analisar as duas expressões separadamente:
Para temos:
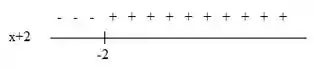
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
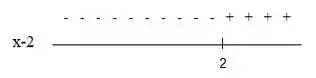
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos analisar agora a situação pedida através das duas imagens que achamos no passo anterior:
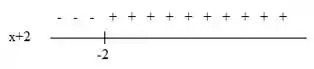
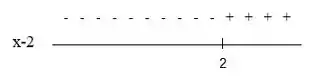
Temos que quando as duas expressões tiverem sinais iguais, analisando as duas imagens vemos que isso acontece quando:
ou
Resposta
para ou