Resolva o problema no Exemplo 4 se o rio tiver de largura e o ponto estiver somente a de rio abaixo.
Passo 1
E aí! tudo certinho?
Nesse problema temos que resolver o exemplo 4 do livro mudando algumas variáveis... agora a largura do rio é e o ponto está a abaixo do rio.
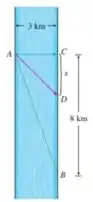
Para relembrar o exemplo 4... ele nos dá esse rio e um homem lança um bote no ponto e deseja chegar no ponto o mais rápido possivel. Ele rema a e anda a e nosso objetivo é determinar o caminho mais rápido dentre as seguintes opções: o homem percorre o caminho , ou .
Tem ideia de como fazemos isso?
Na solução do exemplo, o autor desenvolveu uma equação de tempo em função do deslocamento descrito na imagem do exemplo...
Vamos adaptar essa equação para o nosso caso e aplicar a metodologia que usamos para encontrar os pontos de máximo e mínimo de uma função (derivando e igualando a ).
Bora começar!
Passo 2
A equação desenvolvida pelo autor tem dois termos... o primeiro termo descreve o comportamento do homem sob o rio e o segundo termo descreve o comportamento do homem sob a margem do rio...
Vamos analisar cada termo separadamente...
Quando o homem está remando, ele descreve um movimento que forma um triangulo retângulo
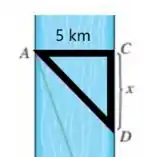
A hipotenusa desse triangulo é a distância percorrida à remo...
Lembra que velocidade é igual ao espaço pelo tempo?
Queremos otimizar o tempo, então podemos dizer que
A distância já temos e a velocidade à remo foi dada... então temos a equação do primeiro termo da nossa função
Tranquilo até aqui?
Passo 3
Agora vamos desenvolver o segundo termo... que é o tempo gasto pelo homem quando ele anda pela margem...
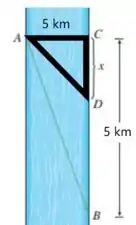
Vamos usar a mesma ideia do passo anterior:
A distância a pé é dada por
E a velocidade por dada no enunciado, ou seja, o tempo gasto andando é
Logo, a equação que descreve o tempo total da movimentação do homem é
Show? Conseguimos encontrar uma função que relaciona o tempo e o deslocamento vertical do barco!
Passo 4
Agora é só cálculo... vamos começar derivando pela regra da cadeia
Igualando a
Vamos elevar os dois lados ao quadrado para simplificar essa raiz...
Isolando
Perceba que , ou seja, está fora do nosso domínio, logo não temos pontos críticos nesse caso, então só nos resta analisar a funç��o tempo nos limites do nosso domínio, ou seja, e .
Sacou?
Passo 5
Primeiro vamos analisar
Então se o homem seguir para o ponto e ir andando até o ponto ele leva .
Agora se
Se o homem for remando direto para o ponto , ele levara , que é menos que o outro caminho...
então para chegar até o mais rápido possivel, ele deve remar diretamente para .
É isso! O que achou? Responde Aí!
Resposta
Ele deve remar diretamente para .