Resolva o problema de valor inicial.
e determine o intervalo de validade da solução.
Sugestão: Para encontrar o intervalo de validade, procure pontos nos quais a curva integral tem uma tangente vertical.
Passo 1
A EDO acima, é do tipo que pode separar para calculcar a solução. A resolução dela é bem parecida com o que fizemos anteriormente em EDO de primeira ordem.
Agora, vamos deixar tudo que tem y de um lado e tudo que tem do outro lado. Antes disso, vamos fazer essa substituição:
Assim, temos:
Passo 2
Agora para termos uma equação dependendo de y e de x, basta integrar dos dois lados
Integrando dos dois lados, temos:
No enunciado há uma informação de que . Vamos escrever a seguir a solução final que encontramos da EDO.
Ao substituir a informação encontramos o valor da constante C. Logo, temos:
Assim, a equação é:
Passo 3
Ou seja, a equação é:
E o intervalo de validade é quando
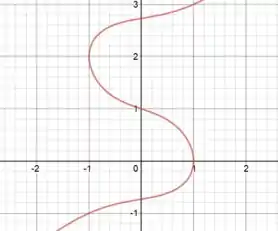
Como vemos no gráfico o intervalo que há uma reta tangente vertical é no período dito acima.