Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 25
Resolva o problema de valor inicial e trace a solução (se seu SCA fizer gráficos implícitos).
Passo 1
Hey, galera! Nessa questão, a gente precisa resolver uma equação diferencial que é separável, veja só:
Passo 2
Como a gente já conseguiu separar cada variável em um lado da equação, basta integrar cada lado:
E aí a gente substitui e um ponto fornecido pelo enunciado, pra achar quem é a constante :
Então ficamos com a equação implícita:
Passo 3
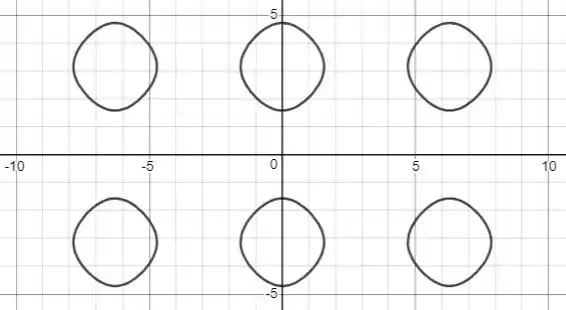
Agora vamos traçar a solução a partir da equação implícita:
Resposta
Exercícios de Livros Relacionados
Em uma reação química elementar, as moléculas únicas de dois reagentes A e B formam a molécula do produto C: A + B → C . A lei de ação das massas afirma que a taxa de reação é proporcional ao produto
No Exercício 28 , na Seção 9.2 , discutimos uma equação diferencial que modela a temperatura de uma xícara de café a 95° C em uma sala a 20° C . Resolva a equação diferencial para encontrar uma expres
Um tanque contém 1000L de água pura. Água salgada com 0,05k g de sal por litro de água entra no tanque a uma taxa de 5L / m i n . Água salgada com 0,04k g de sal por litro de água entra no tanque a um
Um pequeno país tem $10 bilhões em papel-moeda em circulação e a cada dia $50 milhões chegam aos bancos daquele lugar. O governo decide introduzir uma nova moeda, fazendo com que os bancos troquem not
No Exercício 13 , na Seção 9.1 , formulamos um modelo para o aprendizado na forma da equação diferencial d P d t = k M - P onde P ( t ) mede o desempenho de alguém aprendendo uma habilidade depois de