Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.3 - Ex. 37
Resolva o problema de valor inicial no Exercício , na Seção , para encontrar uma expressão para a carga no instante . Encontre o valor-limite da carga.
Enunciado do Exercício :
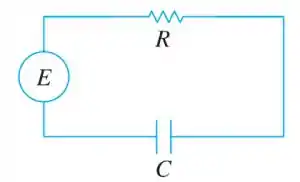
A figura mostra um circuito contendo uma força eletromotriz, um capacitor com capacitância de farads () e um resistor com resistência de ohms (). A queda de voltagem no capacitor é , onde é a carga (em coulombs); nesse caso a Lei de Kirchhoff fornece
Mas , de modo que temos
Suponha que a resistência seja , a capacitância seja e a pilha forneça uma voltagem constante de .
(a) Desenhe um campo de direções para essa equação diferencial.
(b) Qual é o valor-limite da carga?
(c) Existe uma solução de equilíbrio?
(d) Se a carga inicial for , use o campo de direções para esboçar a curva solução.
(e) Se a carga inicial for , use o método de Euler com o passo para estimar a carga depois de meio segundo.
Passo 1
E aê, pessoal, beleza? Nesse exercício aqui, é bastante importante prestar atenção ao que está sendo pedido, se não a gente embola tudo e faz o que não precisa. O enunciado não tá pedindo que a gente resolva o todo de novo, ele quer que a gente resolva o problema de valor inicial.
Mas antes, a gente precisa identificar que problema de valor inicial é esse, pois o exercício não quis nos entregar de bandeja. Repare que o enunciado do nos deu uma equação diferencial:
Mas isso tá tão esquisito, parece que tem mais variáveis do que a gente consegue dar conta de resolver. Aí a gente volta no enunciado, e percebe que e são constantes, o que facilita bastante a nossa vida!
Agora a equação fica melhorzinha:
Então, para completar o problema de valor inicial, só nos falta achar realmente quem é o valor inicial, ou seja, quanto a variável mede quando . Mas dá uma olhadinha nos itens (d) e (e), eles nos deram o seguinte dado:
Pronto! Já sabemos quem é o nosso problema de valor inicial. Bora resolver?
Passo 2
Vamos tentar verificar se nossa equação é separável? Aqui não tem nem , mas faz de conta que o é o , e o é o , não tem nenhuma diferença no método de resolução!
É separável! Que boa notícia! Agora é só integrar cada lado:
Usando a substituição a gente elimina a dificuldade da integral da esquerda:
Passo 3
Show! Encontramos uma solução genérica da equação diferencial, agora vamos usar o fato de que quando para eliminar a constante :
Então nossa equação vai ficando assim:
Porém, a solução com o sinal não obedece a condição inicial, pois teríamos:
Logo, nossa solução é
Passo 4
Achou que já tinha terminado? Ainda não! O exercício também nos pediu pra encontrar o valor-limite da carga. Para isso, é só tomar o limite de quando
Portanto, a carga-limite é , beleza?
Resposta
Valor limite: