Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 23

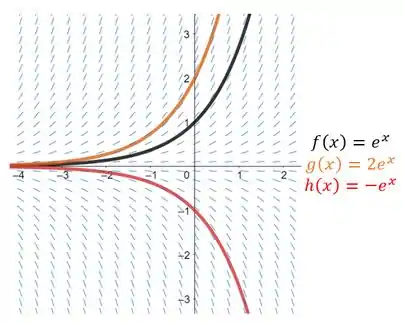
Obtenha um campo de direção e o adicione aos gráficos das curvas integrais que passam pelos pontos dados.

y ' = y

  1. ( 0,1 )
  2. ( 0,2 )
  3. 0 , - 1

Passo 1

Precisamos obter o campo de direções de uma EDO de primeira ordem e depois adicionar as soluções particulares a este campo. Portanto, precisamos realizar o seguinte procedimento:

  1. Obter a solução geral da EDO: o que possibilita obter o campo de direções e as soluções particulares;
  2. Obter cada uma das soluções particulares;
  3. Plotar tudo em um gráfico só através do auxílio de softwares.

Passo 2

Vamos começar por resolver a nossa EDO. Vamos utilizar o método de separação de variáveis (tudo que tem x fica em um membro, junto do d x , e tudo que tem y , junto de d y ). Isto é, se tivermos a seguinte função:

d y d x = f y g x ⟹ d y f y = d x g x

E depois, basta integrar os dois membros. Vamos fazer esta separação de acordo com a nossa função. Sendo assim,

y ' = d y d x = y

d y y = d x

∫ d y y = ∫ d x

ln ⁡ y = x + k

y = e x + k = e x ⋅ e k

y = k 1 ⋅ e x

E esta é a solução geral da nossa EDO! F x = k 1 ⋅ e x .

Passo 3

Vamos obter as nossas três soluções particulares agora. Se a função f ( x ) passa pelo ponto ( 0,1 ) , temos:

f 0 = F 0 = k 1 ⋅ e 0 = k 1 = 1

Logo, k 1 = 1 e f x = e x . Se g ( x ) passa pelo ponto 0,2 , temos:

g 0 = F 0 = k 1 = 2

Portanto, g x = 2 e x . Já se h ( x ) passa pelo ponto 0 , - 1 , temos:

h 0 = F 0 = k 1 = - 1

Portanto, h x = - e x

Passo 4

Agora só nos resta esboçar o campo de direções relativa à EDO dada e plotar as três soluções particulares. Sendo assim, temos:

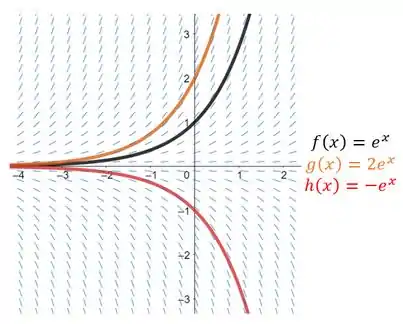
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 5-8, mostre que cada função é uma solução do problema de valor inicial dado.5. Equação diferencial: y ' + y = 2 1 + 4 . e 2 x Condição inicial: y ( - ln ⁡ 2 ) = π 2 Candidata à solução:
Nos Exercícios 5-8, mostre que cada função é uma solução do problema de valor inicial dado.8. Equação diferencial: x 2 y ' = x y - y ² ²Condição inicial: y e = e Candidata à solução: y = x ln ⁡ x
Para todo a0, o gráfico de y=f(x) intercepta ortogonalmente a curva x 2 + 2 y 2 = a . Determine f sabendo que f(1)=2
Para todo a0, o gráfico de y=f(x) intercepta ortogonalmente a curva x y = a . Determine f sabendo que f(2)=3
Um corpo de massa 70 kg cai do repouso e as únicas forças atuando sobre ele são o seu peso e uma força de resistência proporcional ao quadrado da velocidade. Admitindo-se que 1 segundo após o início d