Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 38
Responda o exercício 37 se um dos pedaços é dobrado em um quadrado e o outro em um círculo.
Passo 1
Bom pessoal, nessa questão temos que usar o cálculo para encontrar a menor área possível e a maior área possível.Para encontrar o máximo ou o mínimo de uma função devemos derivar e igualarmos a zero.
E como aqui nós só trabalhamos com uma única variável, caso tenhamos mais de uma variável (nesse caso, temos dois números que queremos encontrar) vamos usar uma equação de restrição para ter uma única variável.
Passo 2
Bom pessoal, temos dois pedaços de fio que somados medem . Um é dobrado em quadrado e outro em circulo. Vamos representar estes pedaços:
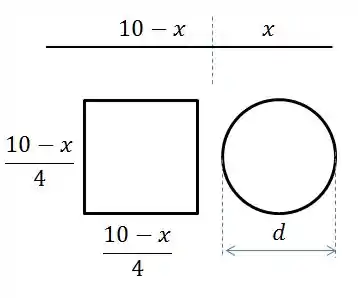
O perímetro do círculo vale o comprimento dividido por 4.
A área do quadrado vale:
A área do circulo vale:
Mas sabemos que o perímetro do circulo vale o comprimento x:
Então:
A área total será a soma das áreas:
Pronto, agora temos uma função que depende de uma única variável.
Passo 3
A letra a) pede a área total máxima:
Os valores críticos de A podem ser encontrados a partir da primeira derivada de A:
Substituindo na equação da área:
Vamos encontrar agora o valor da área nos extremos do intervalo possível de valores para .
Nos outros extremos, quando
Portanto, a maior área é quando todo o fio é usado para o círculo.
- A menor área é o ponto mínimo encontrado: