Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.5 - Ex. 17

Em uma certa cidade a temperatura (em ºC) t horas depois das 9 horas foi aproximada pela função

T t = 20 + 6 . s e n   π t 12

Calcule a temperatura média durante o período entre 9 h e 21 h.

Passo 1

Muito bem, antes de começar vamos lembrar de como se calcula o valor médio da função, ok?

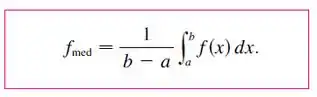
Tranquilo, não é? Durante o período entre 9h e 21h, totalizando 12 horas, então vamos integrar a função de 0 até 12, tudo bem?

Só vamos substituir:

T m e d = 1 12 - 0 ∫ 0 12 20 + 6 . s e n   π t 12 . d t

Vamos separar os termos para integrar separadamente:

T m e d = 1 12 ∫ 0 12 20 . d t + ∫ 0 12 6 . s e n   π t 12 . d t

Tiramos as constantes:

T m e d = 1 12 20 ∫ 0 12 d t + 6 ∫ 0 12 s e n   π t 12 . d t

A primeira já conseguimos resolver, não é?

T m e d = 1 12 20 t + 6 ∫ 0 12 s e n   π t 12 . d t

Para resolvermos a próxima usamos a substituição:

u = π t 12

Derivando:

d u = π 12 d t → 12 π d u = d t

Substituindo:

T m e d = 1 12 20 t + 6 ∫ 0 12 s e n   u . 12 π d u

T m e d = 1 12 20 t + 7 2 π ∫ 0 12 s e n   u . d u

Resolvendo:

T m e d = 1 12 20 t + 72 π ( - cos ⁡ u ) | 12 0

Substituindo u:

T m e d = 1 12 20 t - 72 π cos ⁡ π t 12 | 12 0

Aplicando o intervalo:

T m e d = 1 12 20 × 12 - 72 π cos ⁡ π × 12 12 - 20 × 0 - 72 π cos ⁡ π × 0 12

T m e d = 1 12 2 40 - 72 π cos ⁡ π - - 72 π cos ⁡ 0

T m e d = 1 12 240 - 72 π ( - 1 ) - - 72 π . 1

T m e d = 1 12 240 + 144 π

T m e d = 20 + 12 π

T m e d = 23,8 ° C

Resposta

T m e d = 23,8 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Encontre o valor médio de f no intervalo dado.(b) Encontre c tal que f m e d = f ( c ) .(c) Esboce o gráfico de f e um retângulo cuja área seja a mesma que a área sob o gráfico de f. f x = x ,[ 0
f x = 2 x / ( 1 + x 2 ) ² ,[ 0,2 ] ² a) Encontre o valor médio de f no intervalo dado.b) Encontre c tal que f m e d = f ( c ) .c) Esboce o gráfico de f e um retângulo cuja área é a mesma que a área so
A densidade linear de uma barra de 8 m de comprimento é 12 x + 1 k g m , onde x é medido em metros a partir da ponta da barra. Encontre a densidade média da barra.
Use o resultado do Exercício 79 na Seção 5.5 para calcular o volume médio de ar inalado pelos pulmões em um ciclo respiratório.
Em uma certa cidade a temperatura (em ºC) t horas depois das 9 horas foi aproximada pela função T t = 20 + 6 . s e nπ t 12 Calcule a temperatura média durante o período entre 9 h e 21 h.