Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 5
Responda às perguntas seguintes sobre as funções cujas derivadas são dadas:
- Quais são os pontos críticos
- Em quais intervalos f é crescente ou decrescente?
- Em quais pontos, se houver f assume máximos e mínimos locais?
Passo 1
Primeiro, vamos igualar a zero para encontrar os pontos críticos:
Como nunca é zero, a primeira derivada será zero se, e somente se,
Ponto crítico´: 1
Passo 2
Agora, vamos fazer o estudo do sinal para verificar onde a função cresce e decresce. Beleza?
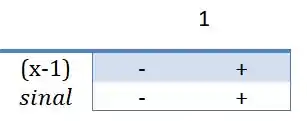
Logo,
é crescente no intervalos (1, +∞)
é decrescente no intervalo (-∞,-1)
Passo 3
No teste da primeira derivada para os extremos locais vale o seguinte:
Seja c um ponto crítico de uma função contínua e essa função é derivável em qualquer ponto do intervalo que contenha c então:
- Se passa de negativa a positiva em c, então possui mínimo local em c ;
- Se passa de positiva a negativa em c, então possui máximo local em c;
- Se não muda de sinal em c, então não tem extremo local em c
Assim, podemos afirmar que não assume valor máximo local e assume valor mínimo local quando (pois nesse ponto a função muda de negativo para positivo)
Resposta
Ei, a resposta está no passo a passo :)