Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.2 - Ex. 48
Se e encontre .
Passo 1
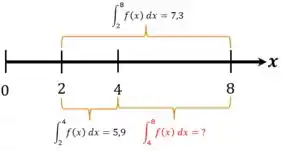
Fala aí, galera! Antes de atacarmos o problema, bora organizar as informações que temos. Queremos encontrar a integral definida , considerando que já sabemos que:
- A integral definida é .
- A integral definida é .
Dando uma olhada nas três integrais abordadas, dá pra ver que os limites de integração satisfazem a relação e, além disso, o integrando de todas é a mesma função .
Então, o que voc�� acha de usarmos a propriedade das integrais definidas que nos permite combinar integrais de uma mesma função em intervalos adjacentes? Parece ser o nosso caso, né? Bora ver como fazemos isso!
Passo 2
Pensa só: a integral da função em todo o intervalo pode ser dividida em duas partes, uma integral no intervalo e outra no intervalo . Mas como expressar isso como uma equação? Não tem mistério:
Como já temos o valor das duas primeiras integrais da igualdade anterior, substituindo esses valores vamos ter que:
Esse conceito é conhecido como aditividade das integrais. Se você curte definições matemáticas, ele pode ser expresso da seguinte maneira: Sejam e . Se é integrável em e em , então também é integrável em e vale que:
Passo 3
Falta pouco para chegarmos à resposta. Na verdade, a gente só precisa isolar a integral que queremos descobrir e fazer a subtração necessária. Checa só: