Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 27

Um retângulo é inscrito num triângulo retângulo de catetos que mede 9   c m e 12   c m . Encontrar as dimensões do retângulo com maior área, supondo que sua posição é dada pela figura a seguir.

Passo 1

Pra começar, vamos fazer uma ilustração do que ele está nos dizendo. Olha só:

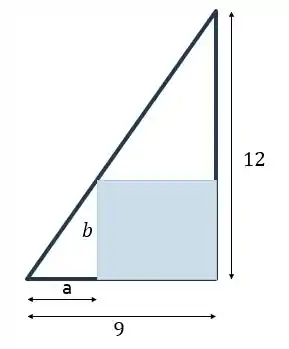
Repare que o triangulo retângulo pequeno é semelhante ao triangulo retângulo grande. Assim,

a b = 9 12

Logo,

a = 3 4 b       ( i )

Passo 2

Como queremos a maior área possível para o retângulo, vamos equacionar essa área e em seguida maximizar!

A = 9 - a × b

Usando a relação ( i ) :

A b = 9 - 3 4 b × b

Fazendo a distributiva:

A b = 9 b - 3 4 b 2

Como a expressão da área é uma equação do segundo grau com coeficiente líder (o que acompanho b 2 ) negativo, então nossa curva terá concavidade para baixo. Assim, haverá um ponto de máximo. Então basta derivarmos e igualarmos a zero que já encontraremos o ponto de máximo.

A b = 9 b - 3 4 b 2

Derivando,

A ' b = 9 - 2 × 3 4 b

Simplificando e igualando a zero:

9 - 3 2 b = 0 → b = 6   c m

Com a equação ( i ) conseguimos achar a . Logo,

a = 3 4 × 6 → a = 9 2   c m

Passo 3

Olhando para ilustração do Passo 1, vemos que a base do retângulo é dada pelo seguinte:

b a s e = 9 - a

Como a = 9 2 :

b a s e = 9 2 c m

Isto é,

b a s e = 4,5   c m

Já a altura ela será igual a b . Assim,

a l t u r a = 6   c m

Resposta

Retângulo de base 4,5   c m e altura 6   c m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem g t =- 3
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem g x = x
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f θ =3 θ
Responda às perguntas seguintes sobre as funções cujas derivadas são dadas:Quais são os pontos críticosEm quais intervalos f é crescente ou decrescente?Em quais pontos, se houver f assume máximos e mí
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f r = 3