Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 25
Um fazendeiro deve cercar dois pastos retangulares, de dimensões e , com um lado comum . Se cada pasto deve medir de área, determinar as dimensões e , de forma que o comprimento da cerca seja mínimo.
Passo 1
Pra começar, vamos fazer uma ilustração do que ele está nos dizendo. Olha só:
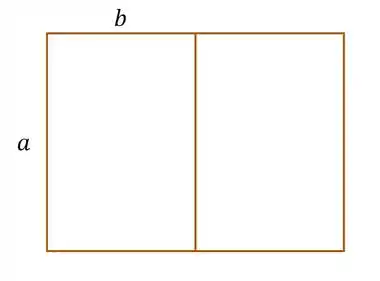
A gente sabe que a área de cada pasto é de . Logo,
Isolando :
Se considerarmos o comprimento total da cerca como :
Substituindo na expressão acima:
Beleza, já temos uma equação para o comprimento da cerca.
Passo 2
Agora vamos derivar e igualar a zero para ver quais são os pontos críticos.
Derivando,
Igualando a zero:
Assim,
Simplificando,
Opa, agora que já sabemos basta voltarmos em e acharmos .
Portanto,
Resposta
Exercícios de Livros Relacionados
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem h x =- x
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem g t =- t
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f x = x